疫学研究が扱う（介入を含む）曝露の中には，パンデミックや政策など，集団レベルで広く影響するものもあります。今回は，集団レベルの曝露効果の推定手法について学びましょう。

集団に影響する曝露の特徴

　本連載でこれまで対象としていた曝露は，薬剤など主に個人レベルで変わり得るものでした。曝露群と非曝露群が存在し，傾向スコア分析などで交絡を調整し，両群のアウトカムの差分を曝露の効果として推定しました。

　しかし，集団レベルで影響する曝露の場合，個人間の影響などをとらえるのは難しく，個人レベルのアプローチが政策示唆を考える上で有用とは限りません。また同時期の同一集団内には対照群がいない状況が多いため，別の集団や曝露開始前の同一集団との比較になります。このような比較を行って集団レベルの曝露効果を推定するには，これまでと違った工夫と仮定を要します。

差分の差分法

　曝露（政策介入など）を受けた集団の他に非曝露群の集団があり，両群にて曝露前後の2時点以上での測定がある場合には，曝露による効果と曝露以前からの群間の違いとを判別できる可能性があります。例えば，ある地域のみに適用される政策介入の，医療費に及ぼす影響を調べたいとします。実際に政策介入を行ったときの医療費と，反事実的にその地域で政策介入を行わなかった場合の医療費を比べたいのですが，その地域で政策介入を行わなかった場合の医療費は観測できていないので，比較できません。

　もし近隣にこの政策介入を行わなかった地域があれば，その地域を対照として比較できるかもしれません。しかし，非適用地域での医療費はもともと適用地域と多少異なるはずなので，非適用地域の結果が適用地域で反事実的に政策介入が行われなかった場合の結果と同様と見なすのは難しそうです。そこで，差分の差分法（Difference-in-differences method：DID法）では，非適用地域での医療費の前後の変化（差分）を適用地域において政策介入が行われなかったときの医療費の変化と見なし，適用地域の実際の変化と比較して（差分を取って）適用地域における因果効果を推定します（図1）。

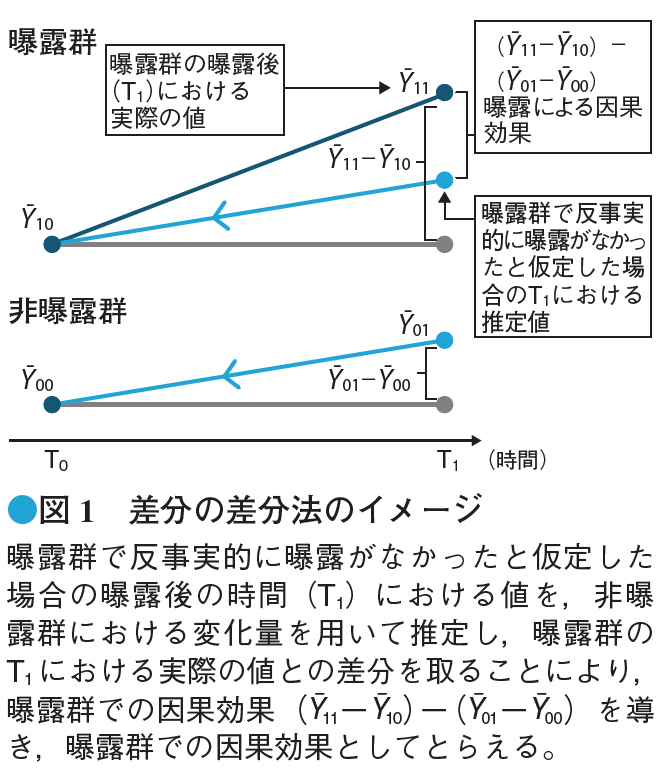
　具体的には，適用地域と非適用地域で介入前後に測定を行い，適用地域による介入前後の医療費の平均をそれぞれȲ₁₀Ȳ₁₁，非適用地域による介入前後の医療費の平均をそれぞれȲ₀₀Ȳ₀₁と表すと，介入前後の変化の差分，（Ȳ₁₁－Ȳ₁₀）－（Ȳ₀₁－Ȳ₀₀）を因果効果として考えます。実際の解析では，Y＝α＋β_XX＋β_TT＋β_XTX^＊T＋……〔X＝曝露（介入），T＝曝露前（＝0）または後（＝1）〕というように，曝露の変数とタイミングの変数，そしてそれらの交互作用項を含めた多変量回帰モデルを作成し，交互作用項のβ_XTを因果効果として考えます。交絡する可能性のある因子は多変量回帰モデルの中で調整します。また，差分を取ることで未測定交絡もある程度調整できると考えられています。ちなみに集団レベルで影響を及ぼす曝露の効果を推定するため，曝露前後で同一個人がいてもいなくても検討できます（註1）。

　差分の差分法による推定が適切に行われるにはいくつかの仮定が必要ですが^1），特に重要なのは「平行トレンド仮定」と呼ばれる仮定です。これは曝露が生じなかった場合には，2測定の差分は同じ，すなわち変化が平行であるとの仮定になります。曝露前の複......