ある曝露によるアウトカムへの因果効果は，対象集団の基本属性（年齢・性別など）や特徴（基礎疾患など）によって異なる場合があり，これを効果の異質性（effect heterogeneity），あるいは効果修飾（effect modification）と呼びます。今回は，この効果修飾について学んでいきましょう。

効果修飾とは何か

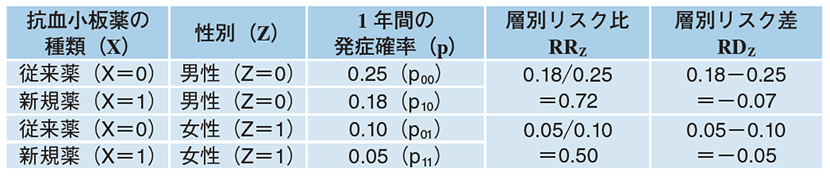
　表に示す架空のデータから，（従来薬と比べた）新規抗血小板薬が再発脳梗塞発症を防ぐ効果について考えてみます。ここで新規薬の効果についてリスク比を指標とした場合，（他に交絡がないと仮定すると）男性における新規薬の効果RR_男性＝0.72，女性における効果RR_女性＝0.50と女性において新規薬の効果が大きいことになります。このような場合に「効果修飾がある」と判断します。

　第5回で少し触れたように，多変量回帰モデルで効果の異質性，すなわちYの関数R（Y）とXの関係がZの値によって変わり得ることをモデル上で考慮するには，XとZの積の項（XZ：交互作用項と呼ぶ）をモデルに含めます。ロジスティック回帰モデルや修正ポアソン回帰モデルなど，ロジットlog〔p/（1－p）〕ないし対数のリンク関数を持つモデルの場合，交互作用項の係数の大きさを見ることで，比を指標とした場合の効果修飾を評価することができます。

　ただし，効果の有無や方向は，指標によって異なり得ることには留意が必要です。リスク差を指標とした場合，RD_男性 ＝－0.07，RD_女性＝－0.05となり，今度は男性の方が新規薬の効果が大きいことになります。得たい効果修飾についての示唆が何かによって，指標をどちらかに選ぶ必要があります。例えば，男女各1000人に新規薬を投与して，脳梗塞の新規発症人数をより多く抑えるのはどちらか？　という問いに答えるには，差を指標とした効果修飾を考慮することになります（註1）。

　なお，効果修飾と交互作用は，同義語として使われる場合が多いですが，狭義では，交互作用は2つとも介入可能な変数の場合のみを指すことがあります。この違いは，どの曝露・介入に関心があるのか？　モデルに共変量として何を含めるか？　得られる示唆は何か？　という議論につながります。詳しくは成書をご覧ください^{1, 2）}。

因果推論における異質性を考慮する

　第7回で述べた逆確率重み付けやG-computationを因果推論の場面で用いると，曝露への介入を観察集団全体に対して行った場合の効果を推定することが多いです。この場合の効果を平均因果効果と呼びます。一方で，例えば第6回で述べた傾向スコアマッチングにおいて曝露群がほぼ解析対象に残った場合には，「曝露群における」平均因果効果を推定していることになります。これらの大きさが異なるのは，属性の分布によって効果の異質性があり，集団全体と曝露群で属性の分布が異なるためです。

　さらには，集団全体をある属性で層別化すると層ごとの推定値が大きく異なり，極端な例では，効果...