前回までは，研究開始時の曝露状況が追跡期間中に変わらないシンプルなシナリオを扱ってきました。しかし実際の研究では，曝露状況が時間とともに変化するケースに出会うことがしばしばあります。例えばコホート研究において，研究開始時にスタチンを内服していた人が，その後のフォローアップで内服を中断していた場合などです。今回は，スタチンを内服継続する場合の3年後の冠動脈疾患発症リスクが，全く内服しない場合のリスクと比べてどの程度下がるか，という経時的な情報を含む臨床の疑問に答えるための手法を紹介します^1～3）。

曝露が時間とともに変化することで生じる問題点

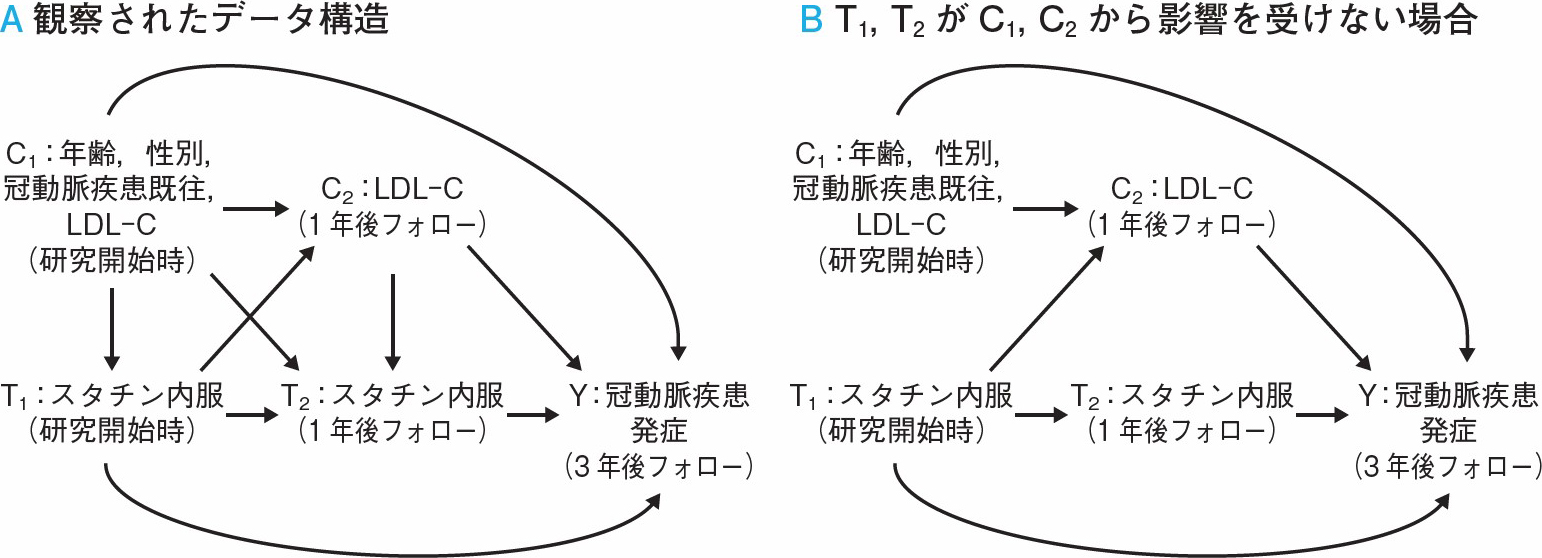
　そもそもなぜ，曝露状況が変化する際に特別な注意を払う必要があるのでしょうか？　この問いに答えるために前回までの連載内容から，調整すべき交絡因子について図1-Aの例で考えてみましょう。コホート研究開始時のスタチン内服（T₁）による冠動脈疾患発症（Y）への因果効果を推定するには，研究開始時の年齢，性別，冠動脈疾患既往，LDLコレステロール値（LDL-C，C₁）を調整することで，バックドア経路（T₁←C₁→Y）を閉じる必要がありました。ここで，1年後フォローのLDL-C（C₂）は中間因子であるため調整することは望ましくありません（第3回参照）。一方で，1年後フォローのスタチン内服（T₂）によるYへの因果効果を求める際には，バックドア経路（T₂←T₁→Y，T₂←C₂→Y）を閉じるために，C₁の他にT₁，C₂でも調整しないとバイアスが生じます。以上から，研究開始時・フォロー時共にスタチン内服していない参加者（T₁＝T₂＝0）と比較して，両時期にスタチン内服している参加者（T₁＝T₂＝1）の冠動脈疾患発症リスクがどの程度下がるかを，T₁，T₂，T₁×T₂を含んだ一般的な回帰モデルで検討するのは困難です。

治療確率による逆確率重み付け（IPTW）

　そこでまず，IPTWのアプローチを紹介します（図2-A）。図1-Aで難しかった点は，T₁にとって中間因子であるC₂が，T₂にとっては調整すべき交絡因子であることでした。一方で...