今回は，多変量回帰モデルの説明と，回帰係数を直接的に因果効果と解釈できるために必要な仮定を説明します。

回帰モデルの基本

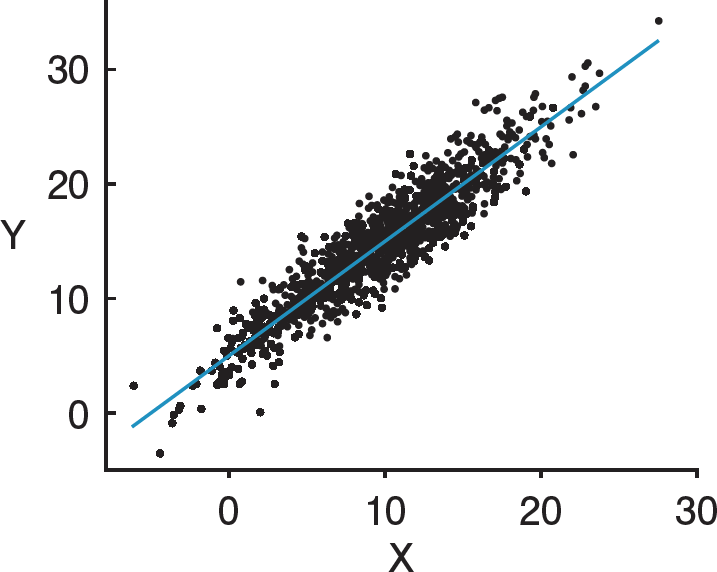
　回帰モデルとは，現実を簡略化し，数式で変数間の関係を表したものです。統計の講義で最初に習う最も単純な回帰モデルはY＝α＋βXという式でしょう。図では散布図の点が標本の観察データを表しています。Xが決まってもYは1つに決まりませんが，回帰モデルを用いるとばらつきに当たりをつけられます。係数βは，「平均して，Xの1の増加は，Yのβの増加と関連がある」ことを意味します。図ではXは連続変数ですが，0または1の2値変数などでも構いません。また，回帰モデルは本来Yを予測するモデルにすぎず，その作成においてXとYの因果関係を想定する必要はありません。

　上記のように説明変数（X）が1つのものを単回帰モデルと呼びますが，複数（例えばXとZなど）の場合は多変量回帰モデルと呼びます。一般に，目的変数（Y）が連続変数の場合，Y＝α＋β_XX＋β_Z1Z₁＋β_Z2Z₂……などの「線形回帰モデル」を用います。一方でYが（0，1）の2値変数の場合には，Yの代わりにY＝1である確率P（Y）で表される関数R（Y）についてのモデルを構築します〔R（Y）＝α＋β_XX＋β_Z1Z₁＋β_Z2Z₂……〕。このように目的変数の型やその分布によって定める関数R（Y）をリンク関数と呼び，Yが従うことを仮定する分布を分布族（あるいは指数型分布族，family）と呼びます。リンク関数と分布族を変えることで線形回帰モデルを応用したモデルを総じて，一般化線形モデル（Generalized Linear Model：GLM）と呼びます。各モデルのβ_Xの解釈を表1に示します。

　なお，R（Y）＝α＋β_XX＋β_Z1Z₁＋β_Z2Z₂＋β_XZ1XZ₁のように，XとZ₁の積の項（XZ₁，交互作用項と呼ぶ）が含まれると，XとR（Y）の関係はZ₁の値による変化をモデルに許すことになります。逆に言えば，交互作用項を含めないモデルの場合，XとR（Y）の関係はZ₁の値によって変化しないとの仮定をモデルに課していることになります。

　現実を簡略化するモデルを作った時点で（正しいかどうかわからない）仮定を課している点に留意が必要です。他にも，R（Y）とZ₁がU字型の関連を有するのにZ₁の一次項しか入っていない〔R（Y）とZ₁の間に直線関係を仮定している〕場合など，モデルが現実をうまく表していないことの総称を「モデルの誤設定」と呼び，正しい推定結果が得られな...