前回の解説では，DAGを用いて変数を整理した上で条件付けなどの調整を行い，「仮想的な介入」の有無を比較する状況を作り出せれば観察研究でも因果効果の推定が可能になると説明しました。今回は具体的に，因果効果をどのように推定するか解説します。

平均因果効果を推定するには

　一般に，個人の因果効果を求めることはできません。そのため私たちは，集団のデータを用いて因果推論を行います。具体的には，反事実的（counterfactual）に集団全員が曝露した（何らかの介入を受けた）場合としなかった（介入を受けなかった）場合のアウトカムを比較し，それら反事実リスクの差（因果リスク差，causal risk difference：因果RD）や比（因果リスク比，causal risk ratio：因果RR）^{1, 2）}などの平均因果効果を推定します。平均因果効果の推定では，まず標的集団が集団全員か，実際に曝露を受けた人たちなど部分集団かを明確にする必要があります。そして，曝露とアウトカムを明確にすることも重要です。

　今回は，アスピリン投与を曝露，5年間の冠動脈疾患発生をアウトカム，冠動脈疾患既往が交絡因子の架空のシナリオ（図，表1）で説明します。標的集団は，冠動脈疾患既往の有無にかかわらず，3000人の集団全員です。

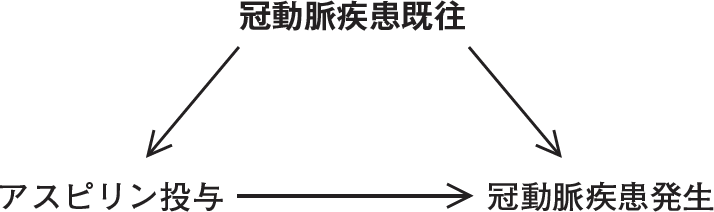
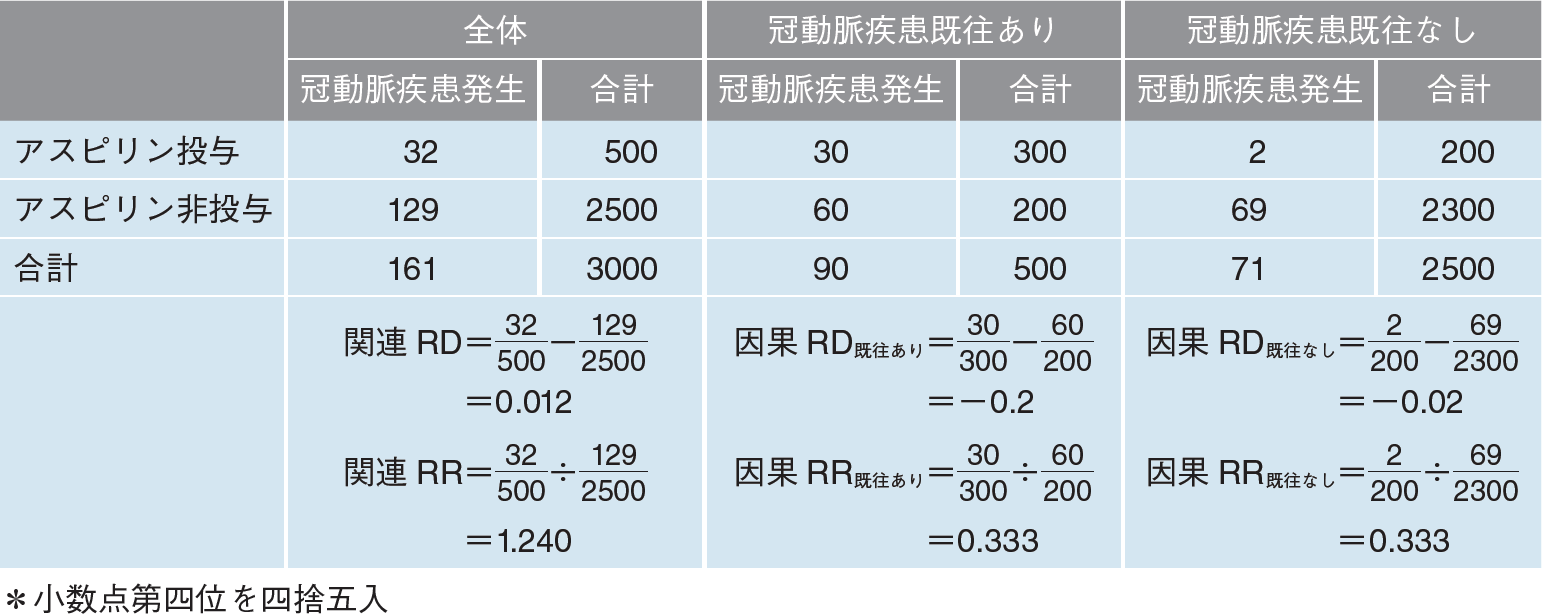
　未調整のRDやRR（関連RD，関連RRと呼ぶ）によると，アスピリン投与と冠動脈疾患発生リスクとの正の関連が示唆されますが，因果RDや因果RRとは異なると考えられます。そこで，冠動脈疾患既往あり群となし群に層別するとアスピリン投与の有無を「仮想的な介入」の有無と見なせるようになり，冠動脈疾患既往ありの層となしの層のそれぞれを標的集団とする因果RDや因果RRを求められます^3）。この層別解析の結果は，アスピリン投与により冠動脈疾患発生リスクが低下したことを示唆しています。

集団全員での平均因果効果の推定

　では，集団全員を標的集団とする平均因果効果はどう推定できるのでしょうか。ポイントは，冠動脈疾患既往で層別すると交絡がないことです。初めに，集団全員にアスピリンを投与したときの冠動脈疾患発生リスクを考えます（表2）。ここでは，実際にはアスピリンが投与されなかった群で冠動脈疾患既往ありの人は...