（第1回のつづき）

変数って何？

さて，続いて「変数」について学習します。

統計解析の学習において，「p値」と並んで重要なのが「変数」の種類を理解することです。これが理解できると（といっても，難しいことではありません），実際の統計解析ができるようになります。

「変数」について，具体例を挙げて説明します。例えば，東京都の高校3年生の男子の身長と，山形県の高校3年生の男子の身長を比較する状況を想定してください。このとき，「身長」は「変数」です。調査対象者ごとに身長の値（○cm）が変わるため，「変化する数値」＝「変数」といいます。このように，身長，体重，血糖値，血圧値など，調査対象者ごとにいろいろな値を取るものが「変数」です。一方，常に一定の値を取るものを「定数」と呼びます。

もう一つ「変数」の例を挙げます。数値ではありませんが，《糖尿病あり》や《糖尿病なし》も「変数」として扱います。なぜなら，調査対象者ごとに《糖尿病あり》であったり， 《糖尿病なし》であったり，変化するからです。数値でないのに変数と呼ぶのはおかしいかもしれませんが，慣習としてそのように呼ばれていますので，そのまま覚えてください。

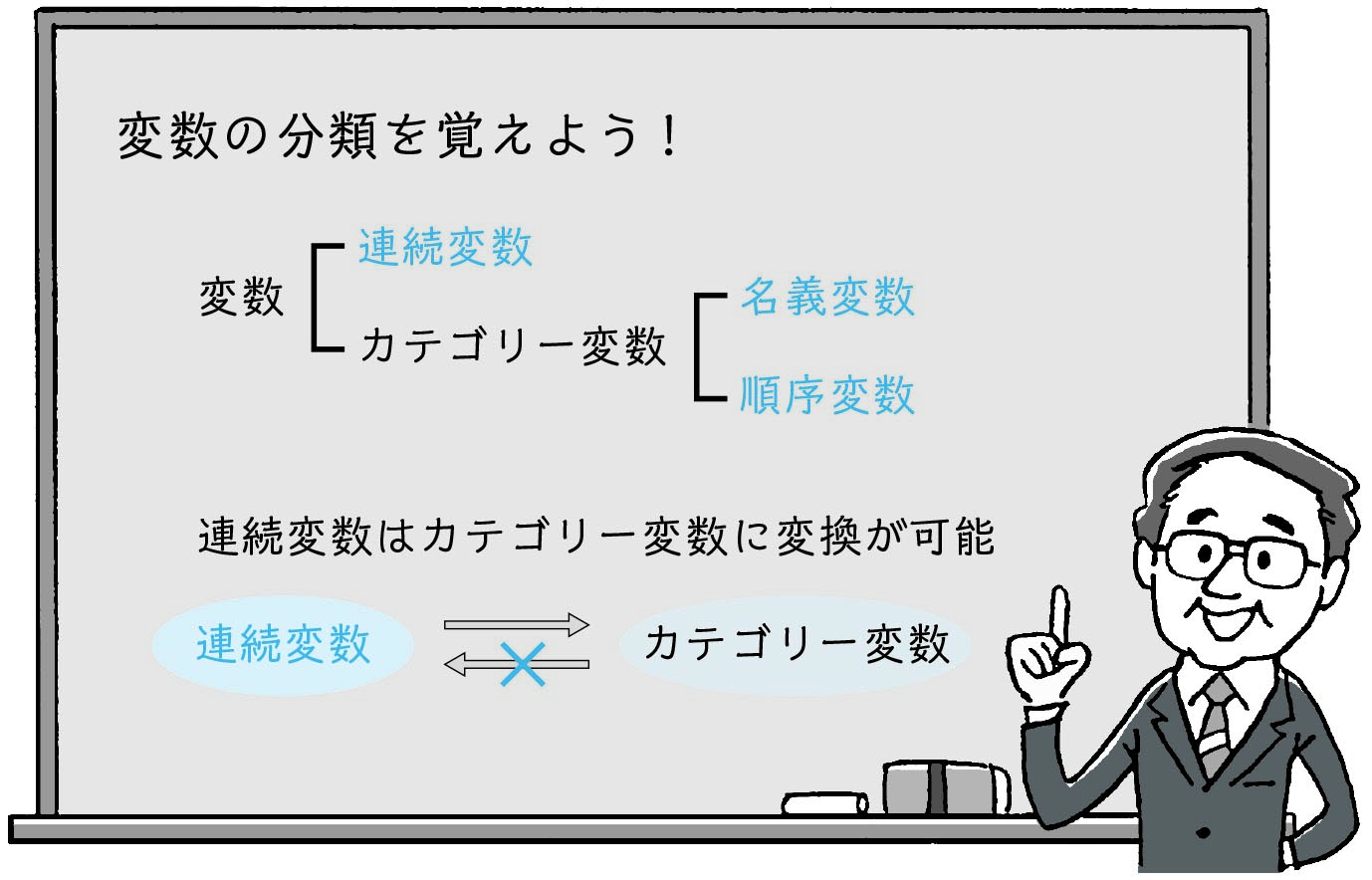
身長，体重，血糖値，血圧値など，連続した数字で表される変数は「連続変数」と呼びます。一方，《糖尿病あり》《糖尿病なし》は2つのカテゴリーで表すことができますが，こうしたカテゴリーで表現できる変数は「カテゴリー変数」と呼びます。後述しますが，カテゴリー変数は「名義変数」と「順序変数」に細分されます。

変数の種類を理解することがなぜ重要か？　それは，変数の種類によって，用いる検定法が異なるからです。

例えば，「t検定」という検定法には「連続変数」しか用いることができません。一方，「フィッシャーの正確検定」や「カイ2乗検定（χ2検定）」にはカテゴリー変数しか用いることができません。個々の検定法については，後程説明しますので，ここでは分からなくても問題ありません。

次に，「変数」について具体例を挙げて解説します（表1-1）。

「連続変数」は連続した数値で表現できる変数です。例えば，身長は「165 cm，168 cm，170 cm，176 cm……」といったように数値で表現でき，その数値により身長の「高い」「低い」を評価できます。同様に，体重も「56 kg，60 kg，63 kg，70 kg……」と連続した数値で表現でき，その数値により体重の「重い」「軽い」を評価できるため，「連続変数」となります。

健康診断や医療機関で行う血液検査は，多くの検査結果が「連続変数」で表現されています。

名義変数
「名義変数」は数字に表せない変数です。例えば，性別，ABO式血液型などです。また，高血圧の有無，糖尿病の有無など，多くの「名義変数」があります。

ここで重要なのは「名義変数」の定義を明確にすることです。例えば，《糖尿病あり》は「HbA1c値が6.5％以上」，《糖尿病なし》は「HbA1c値が6.5％未満」のように，客観的な定義を用いることが重要です。この例の場合には，「日本糖尿病学会の診断基準を参考にHbA1c値が6.5％以上を《糖尿病あり》と定義する」と記載できます。

HbA1c値や血糖値などの検査値がない場合には，「糖尿病の治療を受けている群」と「それ以外の群」の2つのカテゴリーに分けることも可能です。しかし，この場合には客観性が乏しい（「それ以外の群」にも糖尿病患者がいる可能性がある）ので，そのような調査結果や研究は「学術誌」には掲載してもらえない可能性があります。

一般的には，「国際的な診断基準」「わが国の診断基準」「専門の学術学会の診断基準」などに準じて閾値（境界の値，註）を設定します。医学的，理論的に説明できない任意の値で区切ることは許されませんので，くれぐれも注意してください！

順序変数
「順序変数」は数値ではないが順序を伴っている変数です。「名義変数」に似ていますが，順序が伴う点が異なります。「名義変数」の場合には，変数の順序を入れ替えても問題はありません。例えば，「《男性》《女性》」を「《女性》《男性》」に変えても影響ありません。一方，「順序変数」は一定の順序に並んでおり，その順序が意味を持ち，順序を入れ替えることはできません。

例えば，尿蛋白は少ない順に「《－》《±》《＋》《2＋》《3＋》」あるいは多い順に「《3＋》《2＋》《＋》《±》《－》」に並べることは可能ですが，「《3＋》《－》《2＋》《±》《＋》」のように並べることは意味を成しません。数学の好き嫌いも，「《好き》《どちらでもない》《嫌い》」か，その逆の順序に並べるのが自然であり，「《どちらでもない》《好き》《嫌い》」の順序に並べると不自然です。

なぜ順序が重要なのか？　これに疑問を持った方もいると思います。しかし，ここでは深入りしません。学習を進めていけば自然に分かります。

同じ検査項目でも，「連続変数」は「カテゴリー変数」で表すことが可能です。HbA1c値は「5.5％，5.7％，6.1％，6.7％……」のように「連続変数」ですが，この「連続変数」をある「閾値」で区切り，《糖尿病あり》と《糖尿病なし》の「カテゴリー変数」（名義変数）に変換できます。

例えば，日本糖尿病学会の診断基準に準拠し，HbA1c値6.5％以上を《糖尿病あり》，HbA1c値6.5％未満を《糖尿病なし》と定義すれば，《糖尿病あり》と《糖尿病なし》は「カテゴリー変数」（名義変数）になります。さらに，HbA1c値5.9％以下を《正常》，6.0〜6.4％を《境界型》，6.5％以上を《糖尿病》と定義すれば，連続変数（HbA1c値）を3つのカテゴリーに分けることができ，この場合は《正常》《境界型》《糖尿病》という順序がありますので，「カテゴリー変数」（順序変数）になります。

一方，「カテゴリー変数」を「連続変数」に変換することは，一般には不可能です。例えば，《肺がんあり》と《肺がんなし》の「カテゴリー変数」を「連続変数」に変換することはできません。

この理由により，健診や疫学調査では，可能であれば「連続変数」でデータを採取しておいた方が得策です。「『連続変数』を用いる検定法」はもちろん，「連続変数」を「カテゴリー変数」に変換すれば，「『カテゴリー変数』を用いる検定法」も使用可能だからです。健診や疫学調査で「カテゴリー変数」しか収集していないと，「『連続変数』を用いる検定法」を使用することはできません。

それではここで，「変数」の理解を確実なものにするため，次の練習問題1-2を解いてみましょう。

ここまでで「p値」と「変数」について学習しました。これで統計解析を行う下準備はできました。やりましたね！　ここまで来れば大丈夫です。「p値」と「変数」を理解したあなたにとっては，「実際の統計解析」は簡単に理解でき，実践できます。楽しみにしてください。

（第3回へつづく）

---

註：ここでは，「連続変数」を「カテゴリー変数」に変換するときに「境界」となる値。例えば，HbA1cの値を「6.5％以上」と「6.5％未満」で区切るとき，閾値は「6.5％」です。