誰でも統計を活用できるチャンスがある

医師，歯科医師，看護師，保健師，薬剤師，栄養士，理学療法士，臨床検査技師などの保健医療職を養成する学部や学科では，必ず，統計学の授業があります。それは，医療には統計学が必須だからです。そして，統計学は数学から派生した学問ですので，統計学の“原理”を理解するには，数学が必須です。大学は学問をするところですから，まず初めに“原理”を理解し，その原理に基づいて“実践”することが理想的であることに異を唱える人はいないと思います。従って，大学の統計学の授業に「難しい数式」が出てくることは，ある意味，避けられないことです。

一方，現実の世界に目を向けてみると，“原理”は理解していなくても，上手に“実践”できることは数多あります。

身近な例を挙げれば，目の前にある「電卓」がその好例です。私には，電卓が加減乗除を行い，平方根まで計算できる“原理”が全く分かりません。しかし，電卓を上手に活用しています。他には「パソコン」もその類と思います。

「“原理”を理解していなければ，それを活用してはいけないか？」。明らかに「No！」です。一昔前は，統計解析を手計算でやっていました。その時代には，統計学の数式を理解していないと統計解析を実践できませんでした。

現在は，1人1台パソコンを所有し，信頼性の高い統計ソフトが誰でも容易に入手できます。しかも無料で入手可能です（後程，紹介します）。そのような時代には，数学が不得意な人でも，自分の仕事に統計を活用できるチャンスがあってもよいのではないかと思います。

「はじめに」で，「学生時代に，難しい数式が出てきた途端，授業が別世界のように感じられ，それ以降，全く理解できなくなった」と訴える保健師，薬剤師，栄養士などの保健医療職の方が多いと述べました。これは私見ですが，授業を行う統計学の専門家の中には，保健医療のリアルワールドを理解していない人が少なくないように思います。彼らは基本的には数学者ですので，原理の解説を重視することは無理もないと思います。

しかし，保健医療の分野においては，統計学は現実の問題を客観的に理解したり，解決するための一つの手段です。現場で「何が問題なのか」「何を明らかにしたいのか」「何を解決したいのか」という問題意識があって，初めて統計手法は生かされます。

今後は，むしろ，数学嫌いの保健医療職の方が統計手法を身に付け，現場の問題点を認識し，現場から出てきた生のデータを統計解析し，保健医療分野の重要な知見をたくさん発信する時代なのではないかと考えています。

統計解析で何が分かるの？

それでは，統計解析ができると何が分かるのでしょうか？

例えば，住民を「塩分摂取量の多い」群と「塩分摂取量の少ない」群の2群に分け，各群の「高血圧の有無」を調査し，統計解析をすると，「2群間で高血圧の有病率に（偶然ではなく）有意な差があるかどうか」が分かります。つまり，2群間（あるいは3群間以上）の「検査値」や「有病率」などに有意な差があるかどうかが分かります。

（偶然では起こりにくい）有意な差があるかどうかの「判断の指標」として重要なのがp値です。本書の読者は統計解析の初心者だと思いますので，本書では「2群間に違いがあるかどうか」の解析を中心に解説します。これがマスターできれば，3群間以上の解析は簡単に習得できるからです。

まず初めに「p値の意味」を学び，次に「変数の種類」を学んでいただきます。「p値の意味」は，統計解析の結果を解釈するのに必要な知識であり，「変数の種類」の知識は，検定法を選択（多数の検定法の中から適切な検定法を選択）するのに必要だからです。

p値って何？

前述のように，統計解析の主要な目的の一つは「p値を算出する」ことと言っても過言ではありません（算出といっても，実際に人が計算するわけではなく，パソコンが自動的に算出してくれます）。統計解析を行っている人は，算出されたp値が大きい値か小さい値かにより一喜一憂します。まず，p値の意味を知りましょう。

ほとんど全ての統計の教科書では，p 値を説明するために，帰無仮説と対立仮説の説明から始めるのですが，ここでは帰無仮説と対立仮説という用語を使用せずにp値を説明します。

 

まず，下の練習問題1-1を見ながら理解していきましょう。

ひとこと　p＜0.05に理論的根拠があるわけではない

p＜0.05に理論的根拠があるわけではないので，論文やレポートでは，必ず「本研究では，p＜0.05を統計学的に有意差ありとする」と一言加えるのが慣習（作法）です。

ひとこと　「有意差がある」は必ずしも「意味のある重要な差異」ではない

「有意差がある」は，必ずしも「意味のある重要な差異」を意味するものではありません（図1-2）。

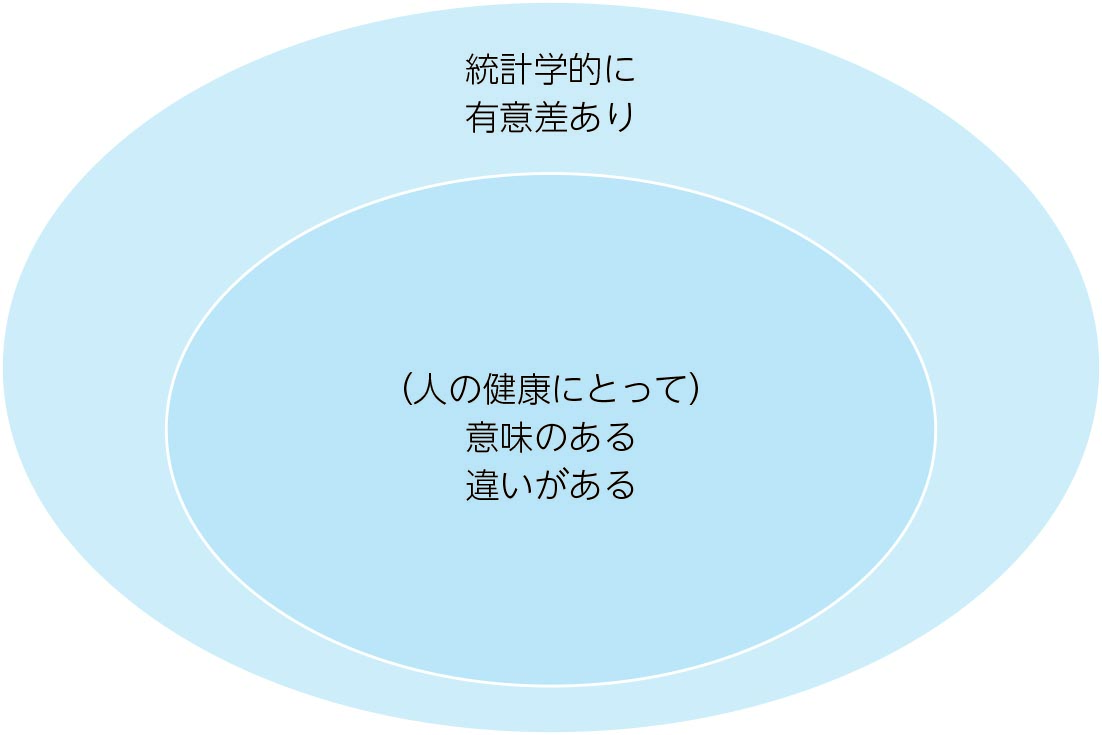
図1-2　「統計学的に有意差あり」と「（人の健康にとって）意味のある違いがある」は，必ずしも同じではない［画像はクリックで拡大］

例えば，A地区の40歳以上の女性の血清総コレステロール値の平均値は210 mg/dL，B地区では220 mg/dLであり，統計解析の結果，p値は0.03であったとします。この場合，「B地区の女性は，A地区の女性に比べ，血清総コレステロール値の平均値は有意に高い（p＝0.03）（＝血清総コレステロール値の平均値は，両群間で有意差がある）」と記載しますが，平均値210 mg/dLと220 mg/dLの違いが，ヒトの健康にとって意味のある違いであるか否かは不明です。

従って，「統計学的に有意な差（有意差）」があった場合には，医学，生物学，社会医学や一般常識などの知識を総動員して，広い視野から「（ヒトの健康にとって）意味のある差」かどうかを検討し評価する必要があります。一方，統計学的に有意差がなければ，それ以上のことは何も言えません。

ひとこと　「有意差がない」＝「違いがない」ではない

最近は少なくなりましたが，学会発表で「統計解析の結果，p値が0.05以上であったので，A群とB群には違いがない」と結論する演題を聞くことがあります。

p＜0.05を統計学的に有意差ありと定義した場合，p≧0.05のときは，「A群とB群に有意差はない」と言えますが，「A群とB群に違いがない」や「A群とB群は同じだ」とは言えません（つまり，A群とB群が同じか違うかは不明⇒判断は保留）。

ひとこと　p値は定量的な差の大きさを示すものではない

A群とB群の検査値（例えば，血圧の測定値）や有病率（例えば，糖尿病者の割合）を比較した場合，「検査値や有病率の差が大きく」てもp値が小さいとは限りません。逆に，多数例を解析したものではA群とB群の差が偶然に起こる確率が小さくなり，「検査値や有病率の差が小さく」ても「p値が小さく」なることがあります（後で学んでいきます）。

つまり，p値が小さければ，「A群とB群に差がある」との結論の確からしさが高くなりますが，群間の定量的な差を表すものではありません。

 

（第2回へつづく）