グラフの読み方・使い方(新谷歩)
連載
2012.02.27
医療統計学講座
【Lesson10】
グラフの読み方・使い方
新谷歩(米国ヴァンダービルト大学准教授・医療統計学)
(2963号よりつづく)
臨床研究を行う際,あるいは論文等を読む際,統計学の知識を持つことは必須です。
本連載では,統計学が敬遠される一因となっている数式をなるべく使わない形で,論文などに多用される統計,医学研究者が陥りがちなポイントとそれに対する考え方について紹介し,臨床研究分野のリテラシーの向上をめざします。
百聞は一見に如かず。グラフは,データをより深く理解するためにも,研究結果を読者に伝えるコミュニケーションツールとしても重要です。今回は統計解析で欠かせないグラフについて説明します。
■グラフ中のエラーバーは何を意味しているか
血圧,コレステロール値などの連続変数をグループ間で比較する際,それぞれのグループのアウトカムの平均を示した棒グラフやエラーバー,箱ひげ図など,さまざまな種類のグラフを目にします。それぞれのグラフをいつ,どのように用いるのか,一つ一つ見ていきましょう。
図1は,アウトカムをA群とB群で比較するために平均を示した棒グラフです。棒グラフからは「B群のアウトカムの平均値がA群よりも高い」という情報は得られますが,その平均が信頼に値する正確なものかといった情報はまったく含まれていません。例えばその平均が,被験者数10人のデータから得られたものなのか,1000人のデータから得られたものなのかで結果の正確性はまったく変わってきます。
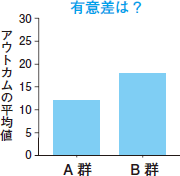 |
| 図1 棒グラフ |
データの正確性を表すために棒グラフにエラーバーのついた図をよく見かけます。図2は,図1と同じデータで標準誤差(SE)のエラーバーを棒グラフに加えたものです。さあ,ここで問題です! この図から,「アウトカムの平均値は2つのグループで統計的に有意差がある」と言えるでしょうか?
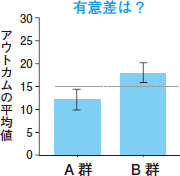 |
| 図2 棒グラフと標準誤差のエラーバー |
2つのエラーバーが重ならないという理由で「有意差がある」と判断した人は要注意です。エラーバーが重なるか重ならないかで判断してよいのは,信頼区間についてのエラーバーが示されているときです(註)。通常用いられる95%信頼区間はSEの約2倍なので,この図でエラーバーを2倍すると2つのエラーバーはどうやら重なってしまいそうですね。このデータでは,スチューデントのt検定でP値を計算したところP=0.13となり,有意差は見られませんでした。
図3は,標準偏差(SD)を表すエラーバーが棒グラフに加えられたものです。SDのエラーバーは集めてきたデータのばらつきを示すので,データが正規分布に従っているとき,約3分の2の被験者のアウトカムの値がエラーバーで示された範囲内に入っていると理解できます。また,SDの2倍のエラーバーの範囲内に約95%の値が入っていると理解します。SDはデータの記述に適していますが,平均の推定比較には適しません。図3のグラフに用いられたデータの場合,2つのエラーバーはかなり重なっていますが,2群のアウトカムの平均を比べるP値は0.003で有意差があると言えます。
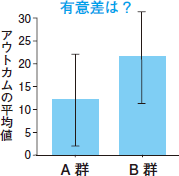 |
| 図3 棒グラフと標準偏差のエラーバー |
このように,エラーバーを用いた比較は,そのエラーバーが何であるかによって,2群間に統計的な差があるかどうかの判断基準がかなり異なります。そのため,エラーバーを使ったグラフには,そのエラーバーが何であるかを図上または説明文中に記載する必要があります(残念ながら,多くのグラフには記載されることなくエラーバーが用いられていることが多いようです)。さらに,論文や学会発表などでT字のエラーバーの上半分だけを棒グラフの上に載せたグラフを大変よく目にします。これはダイナマイトプロットと呼ばれるグラフです。片側だけのエラーバーでは重なるかどうか判断しづらいことから,あまり良いグラフとは言えません。
■箱ひげ図の読み取り方
エラーバーを用いたグラフは,データが左右対称に分布していない場合でもエラーバーは平均の上下に対称に示されるので,データの分布を正確に表すことができません。そこで,エラーバーや棒グラフに置き換わるものとして最近よく見かけるようになったのが箱ひげ図です。
図4は,図1,2で用いたデータを箱ひげ図を用いて表したものです。Q1は25パーセンタイル値,Q2は中央値,Q3は75パーセンタイル値を示します。Q1からQ3までを四分位範囲(Inter Quartile Range;IQR)と呼び,被験者の50%のアウトカム値がこの範囲に入ることを示します。パーセンタイルとは,データを小さい順に並べたときに各値が前から数えてどの位置に来るかを表したものです。例えば,子どもの身長を例にとると,25パーセンタイルは100人の子供が身長の低い順から並んだときにちょうど25番目に並ぶ子どもの身長を表します。中央値は50パーセンタイルと同値で,ちょうど真ん中に来る子どもの身長を表しています。
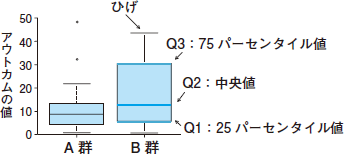 |
| 図4 箱ひげ図 |
箱ひげ図の“箱”がIQRを示すことはわかりましたが,それでは“ひげ”は何を表すのでしょうか? 箱の上に伸びている“ひげ”は,75パーセンタイル値(Q3)に箱の長さの1.5倍を足した値よりも小さな範囲内に存在するデータの最大値を表します。同様に,箱の下に伸びている“ひげ”は25パーセンタイル値(Q1)から箱の長さの1.5倍を引いた値よりも大きな範囲内に存在するデータの最小値を示します。ひげの外にあるデータは外れ値として表されます。
図4の箱ひげ図では,中央値が75パーセンタイル値よりも25パーセンタイル値に近く,上側のひげも長いこと,外れ値もアウトカムの大きい値で存在することなどから,データが上下対称の正規分布に従っているのではなく,低い値に向かって歪んでいることがわかります。また,最近の傾向としてはドットプロットと呼ばれるデータの値を直接ドットで表す散布部のようなグラフと箱ひげ図などを組み合わせ,データの詳細がより具体的に示せるグラフもよく使用されるようになっています(図5)。図1,2,4,5はまったく同じデータから作られたグラフですが,図1,2で示された平均値は図4,5の中央値よりかなり大きくなっています。上下が対称な正規分布に沿ったデータでは平均値と中央値が一致するのですが,このデータのように一方に歪んだデータでは,歪みによって生じた外れ値が平均の計算に影響を及ぼすため,誤った比較をしてしまうこともあります。
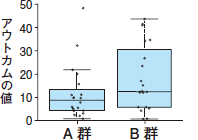 |
| 図5 箱ひげ図とドットプロット |
このように,どのグラフを用いるかで読者に伝わる情報量がかなり異なることがおわかりいただけたでしょうか。たかがグラフ,されどグラフです。限られたスペース内にどれだけ多くの有意義な情報量を詰め込めるかでグラフの良し悪しが決まると言えます。
|
(つづく)
註)厳密には,この基準はデータの特性によっても使えない場合があるので,ここでは大まかな目安として考えてください。
Cumming G, et al. Error bars in experimental biology. J Cell Biol. 2007; 177 (1) : 7-11.
いま話題の記事
-
忙しい研修医のためのAIツールを活用したタイパ・コスパ重視の文献検索・管理法
寄稿 2023.09.11
-
人工呼吸器の使いかた(2) 初期設定と人工呼吸器モード(大野博司)
連載 2010.11.08
-
連載 2010.09.06
-
事例で学ぶくすりの落とし穴
[第7回] 薬物血中濃度モニタリングのタイミング連載 2021.01.25
-
寄稿 2016.03.07
最新の記事
-
医学界新聞プラス
[第4回]脆弱性骨盤骨折
『クリニカル・クエスチョンで考える外傷整形外科ケーススタディ』より連載 2024.04.26
-
医学界新聞プラス
[第3回]わかりやすく2つの軸で分類して考えてみましょう
『心理社会的プログラムガイドブック』より連載 2024.04.26
-
医学界新聞プラス
[第1回]平坦な病変 (1)色調の変化があるもの
『内視鏡所見のよみ方と鑑別診断——上部消化管 第3版』より連載 2024.04.26
-
医学界新聞プラス
[第1回]心エコーレポートの見方をざっくり教えてください
『循環器病棟の業務が全然わからないので、うし先生に聞いてみた。』より連載 2024.04.26
-
医学界新聞プラス
[第1回]バルーン閉塞下逆行性経静脈的塞栓術(BRTO)
『IVRマニュアル 第3版』より2024.04.26
開く
医学書院IDの登録設定により、
更新通知をメールで受け取れます。