医学界新聞プラス
［第4回］名義変数の解析をやってみよう②
『数式不要！はめ込み統計学　EZRでできる保健医療統計これだけ』より

連載加藤丈夫

2021.10.22

数式不要！はめ込み統計学　EZRでできる保健医療統計これだけ

ビッグテータの考え方が広まり，近年ますます重要視されている統計学の知識。しかし，「統計学って複雑な数式を駆使するイメージがあって難しそう」と苦手意識を抱く方も多いのではないでしょうか？　この度上梓された『数式不要！はめ込み統計学 EZRでできる保健医療統計これだけ』では数式を使わず，保健医療の現場で使う実践的な統計手法がわかりやすく解説されています。無料統計ソフト「EZR」を用いた解析の手法の一端を全4回にわたり覗いてみましょう。

（第3回のつづき）

それでは，フィッシャーの正確検定の知識・技術をさらに確かなものにするため，さらに練習問題2-2を解いていただきます。先に述べたように，フィッシャーの正確検定だけで保健医療領域で必要な統計解析の多くが実施可能です。何も参考にせず，ご自身の力でEZRを用いて解いてみてください。

練習問題2-2

A市の国民健康保険に加入している男性を調査した結果，糖尿病などの生活習慣病がなかった方は1,095人いました。しかし，その中の398人には腹部肥満がありました。この1,095人全員を5年間追跡調査したところ，「腹部肥満のある人」から26人，「腹部肥満のない人」から13人が糖尿病を発症しました。　

このデータから，腹部肥満は，その後5年間の糖尿病発症のリスクと言えますか？　

なお，わが国の特定健康診査および日本肥満学会の診断基準に準拠し，男性の腹囲（臍レベル）が85 cm以上のとき，「腹部肥満あり」と評価しました。糖尿病の診断基準は日本糖尿病学会の基準に準拠し，HbA1c≧6.5％としました。

検定法選択
「《腹部肥満あり》《腹部肥満なし》」「《糖尿病あり》《糖尿病なし》」は共に名義変数ですので，「フィッシャーの正確検定」を用います。

分割表作成
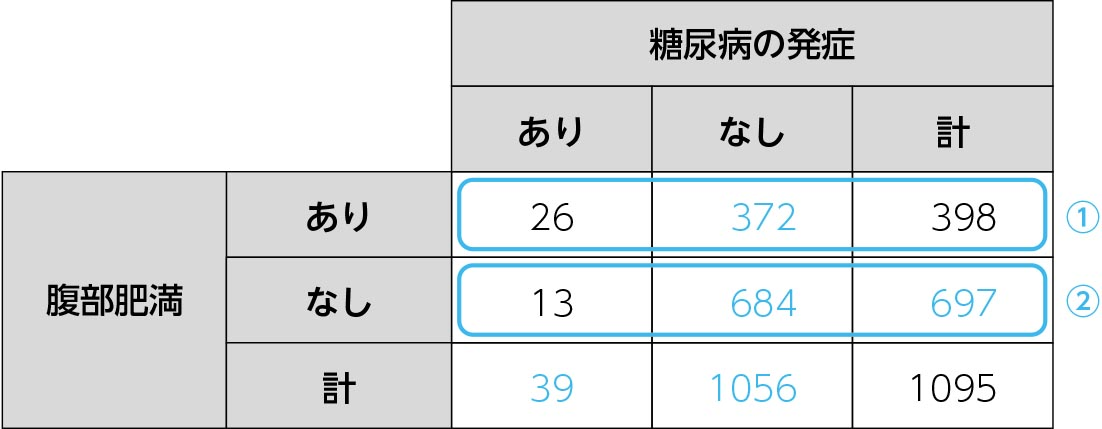
まず，表2-2のように2×2分割表を作成します。なお，「腹部肥満」と「糖尿病」の位置は逆でも構いません。これについては，コラム3で解説します。

《腹部肥満あり》は398人です。腹部肥満ありから糖尿病発症は26人（6.5％）ですので，腹部肥満ありから糖尿病を発症しなかった人は372人（＝398－26）です（表2-2の①）。

《腹部肥満なし》は697人（＝1095－398）です。腹部肥満なしから糖尿病発症は13人（1.9％）ですので，腹部肥満なしから糖尿病を発症しなかった人は684人（＝697－13）です（表2-2の②）。

解析
これをEZRを用いて解析します。EZRを立ち上げ，以下の順に選択します。

　　Rコマンダー　タブ「統計解析」＞「名義変数の解析」＞「分割表の直接入力と解析」

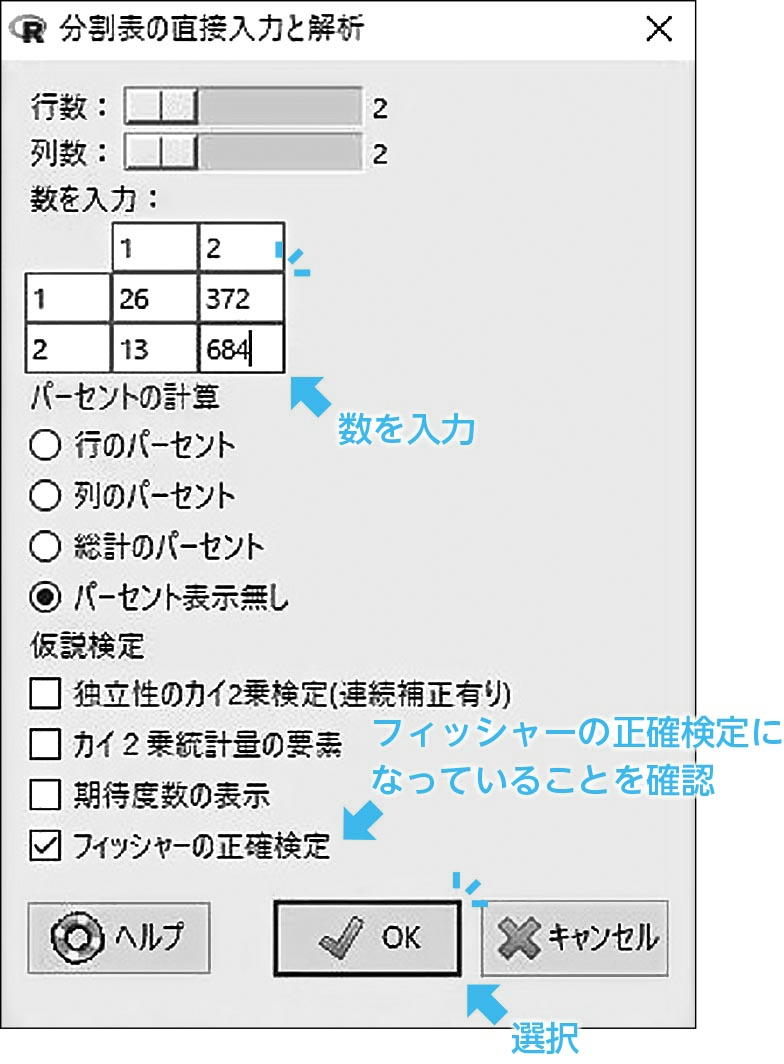
次に現れる画面の空欄の2×2分割表に数字を入れ，「OK」とします（図2-9）。

すると，Rコマンダーの出力欄に結果が表示されます（図2-10）。p値は「0.000122」ですので，有意基準であるp＜0.05を満たします。

結論
従って，「腹部肥満のある人は，腹部肥満のない人に比較して，5年間の糖尿病の発症は有意に多い（p＝0.000122）」と結論できます。

ひとこと　年齢差があれば年齢調整の必要性も考慮

この練習問題に記載されている情報だけを用いて統計解析をすると，前述の結論が得られます。しかし，よく考えてみてください。糖尿病は年齢が高くなるにつれて発症率が高くなります。従って，もし「腹部肥満のない」群に比べ，「腹部肥満のある」群の平均年齢が有意に高ければ，今回の解析で糖尿病の発症率に有意差が出たのは，両群間の「年齢差」による可能性も否定できません。

このような場合，両群間の年齢を調整して解析する必要があります。その方法については，いずれ解説します（p.66）。ここでは，頭の片隅に入れておいていただければ結構です。

もう一題，練習問題をやってみましょう。この練習問題2-3は私が家族と一緒にとあるテーマパークに遊びに行ったときに，空いた時間を利用して実際に私が現場で調査した結果を提示します（調査と言えるものかどうかは分かりませんが）。

練習問題2-3

とあるテーマパークの利用者の男女差を調査するため，ある平日の日中12時10分〜12時20分までの10分間に退出ゲートを通って退場する人を調べました。その結果，成人男性は13人，成人女性は35人，小児は9人でした。

問1：退場した人数に有意な男女差はありますか？
問2：また，このデータを使ってテーマパークの利用者全体の男女差を推測することには無理があります。それをこの調査の限界（limitations）と呼びます。本調査の限界を列挙してください。

検定法選択
まず，小児は外見上，性別が明らかでない場合もありますので，調査対象に入れません。この例では，《実際に得られた人数》と《男女比が等しい状態の人数》について，《男性》《女性》の人数差を検討していきます。これらは共に名義変数ですので，「フィッシャーの正確検定」を用います。《男女比が等しい状態の人数》とはどういうことでしょうか？　2×2分割表を作成しながら見ていきましょう。

分割表作成
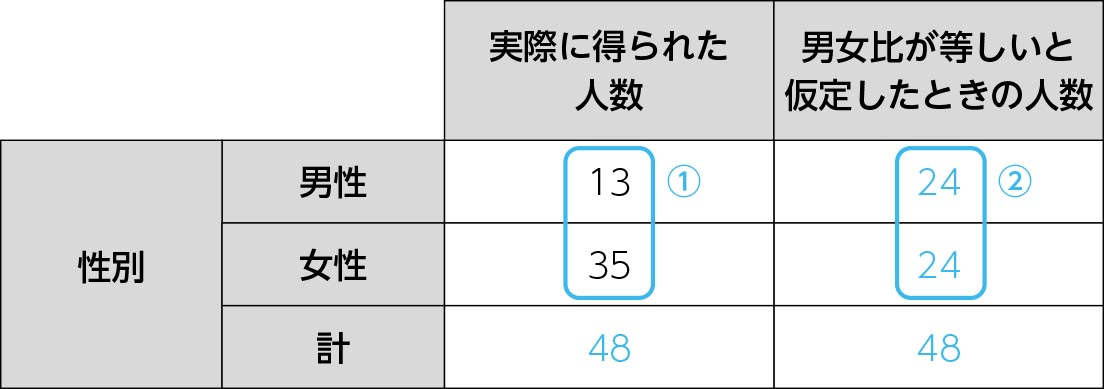
《男性》は13人，《女性》は35人ですので，表2-3の①のようになります。問題は表2-3の②に入れる数字です。もし，男女の割合が等しければ，合計人数が48人（＝13＋35）ですので，《男性》も《女性》も各24人になるはずです。従って，「実際に得られた人数（《男性》13人，《女性》35人）」を「男女比が等しいと仮定したときの人数（《男性》24人，《女性》24人）」と比較し，両者に統計学的に有意な差があるかどうかを検定します。

解析
これをEZRを用いて解析します。EZRを立ち上げ，以下の順に選択します。

　　Rコマンダー　タブ「統計解析」＞「名義変数の解析」＞「分割表の直接入力と解析」

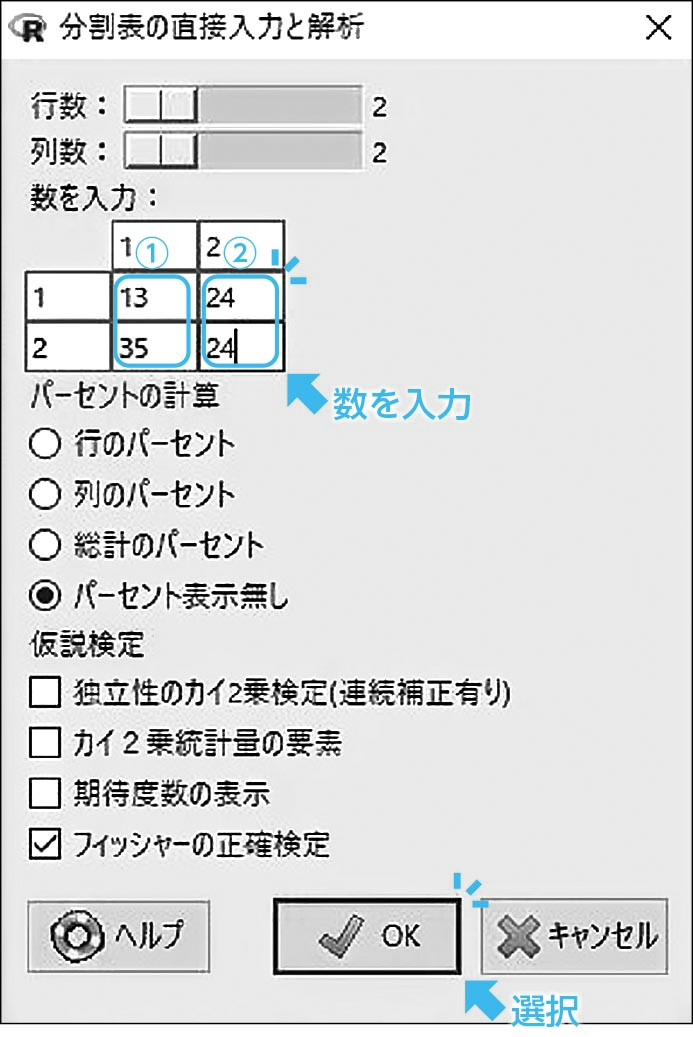
このお決まりの操作を行うと，図2-11の「分割表の直接入力と解析」画面が表示されます。「OK」とすると，Rコマンダーの出力欄に結果が表示されます（図2-12）。

「p＝0.0353」が得られ，これはp＜0.05ですので，両者間には有意な違いがあると評価できます。

結論
従って，「ある日の日中12時10分〜12時20分までの10分間にとあるテーマパークの退出ゲートを通って退場した人は，成人男性に比べて，成人女性が有意に多い（p＝0.035）」と結論できます。

次に問2の調査結果から全体像を推測することの限界を考察します。この調査は，「ある平日の昼時の10分間」に採取したデータです。それも，1回の調査です。この結果から「テーマパークの利用者全体の男女差」を推測することには限界があります。考えられる限界を以下に列挙します。

・平日でなく休日に調査すれば，結果が異なる可能性
・昼時の10分間でなく別の時間帯に調査を行えば，結果が異なる可能性
・調査の時期（季節）を変えれば，結果が異なる可能性
・別のゲートで調査を行えば，結果が異なる可能性
・複数回の調査を行えば，結果が異なる可能性
・小児を含めて聞き取りを行えば，結果が異なる可能性　など

ひとこと　正しい情報提供には「調査の限界」の考察が不可欠

学術論文では，「調査の結果，明らかになったこと」を明記・強調することはもちろんですが，「調査の限界（limitations）」についても考察して言及しないと，学術誌には採択されません。住民に正しい情報を提供し，正しい解釈を促すためには，そして何よりも誤解を与えないためには，行政機関の調査報告書にも「調査の結果，明らかになったこと」だけでなく，「調査の限界」を付記するようにしましょう。　

そのような誠実な姿勢（ある意味，当たり前の姿勢）で仕事をすることが，住民から信頼される行政になるための最低条件であることは間違いないと思います（2019年1月にマスコミを賑わした厚生労働省の不適切統計事件から思うこと）。

コラム　後ろ向き調査（研究）と前向き調査（研究）

調査（研究）手法には，大きく分けると，「後ろ向き調査（研究）」と「前向き調査（研究）」があります（図ⅰ）。

図ⅰ　後ろ向き調査（研究）と前向き調査（研究）

図ⅰの左に示すように，後ろ向き調査（研究）というのは，現在から過去にさかのぼって調査します。例えば，「肺がん」と「喫煙」との関連を調査する場合，後ろ向き調査（研究）では，現在の肺がんの有無を調査し，《肺がんあり》群と《肺がんなし》群の喫煙歴を過去にさかのぼって調査します。そして，両群間で喫煙歴の頻度に有意な差があるかどうかを検定します。

このような調査（研究）を「症例・対照研究（case-control study）」とも呼び（本例では，《肺がんあり》が「症例」，《肺がんなし》が「対照」），後ろ向き調査（研究）の代表です。なお，「過去にさかのぼって調査する」ことを「後ろ向き」と表現します。

このような後ろ向き調査（研究）を2×2分割表にする場合，私は図ⅱの2×2分割表を作っています。こうすると，調査の順序（肺がんの有無の調査→喫煙歴の調査）が一目で分かるからです。しかし，ルールはないようで，肺がんと喫煙の位置を逆にしても検定結果に違いはありません。試しにやってみてください。

　　
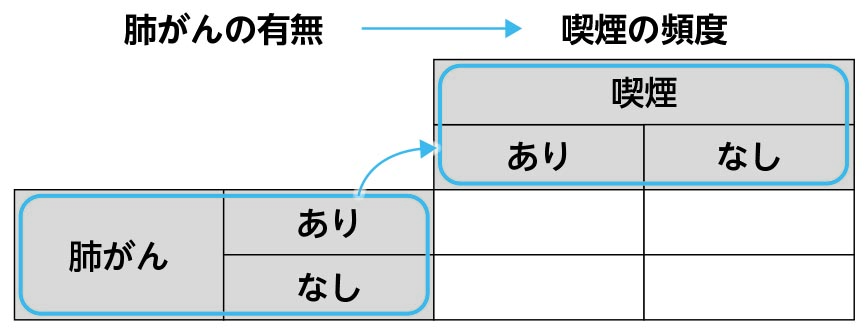
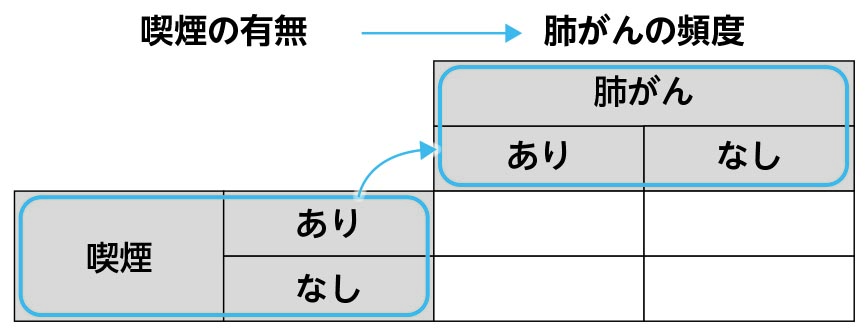
図ⅱ 後ろ向き研究（調査）を2×2分割表にする場合 　　 図ⅲ 前向き研究（調査）を2×2分割表にする場合

一方，図ⅰの右に示すように，前向き調査（研究）では，対象者の現在の喫煙（あるいは喫煙歴）の有無を調査し，未来に向かって追跡調査し，ある時点（例えば，5年後とか10年後）までの肺がん発症の頻度を《喫煙》群と《非喫煙》群で比較・検討します。「未来に向かって調査する」ことを「前向き」と表現します。また，このような調査（研究）を「前向きコホート研究」とも呼びます。後ろ向き調査（研究）と同様に，前向き調査（研究）を2×2分割表にする場合，私は図ⅲの2×2分割表を作っています。

前向き調査（研究）に比較して，後ろ向き調査（研究）は，①短時間で結果を出すことができ，②調査費用も比較的少なくて済むので，後ろ向き調査（研究）が好んで用いられます。しかし，得られた結果のエビデンスレベルは，一般に前向き調査（研究）の方が高いとされています（図ⅰの下）。

今回の連載では，名義変数の解析として「フィッシャーの正確検定」を紹介しました。この検定だけでも多くの保健医療統計が可能となります。例えば，運藤習慣や治療と疾患発病の関係など，身近な数値を用いて統計解析してみてください。
　
書籍『数式不要！　はめ込み統計学』は，こうした名義変数の解析から連続変数の解析，傾向・相関，多変量解析を紹介し，「保健医療統計がこれ1冊でできるように」という趣旨で執筆されました。さらに学習したい方は，ぜひ手に取っていただければ幸いです。

数式不要！はめ込み統計学
EZRでできる保健医療統計これだけ

無料統計ソフトEZRを使って始める保健医療統計！
名義変数の解析から多変量解析まで

＜内容紹介＞保健医療の現場で実際に統計を「使える」ことを目指し，数式を使用せずに解説した実用統計書。運動習慣と糖尿病，喫煙と肺がんなどを題材にした練習問題を基に，無料統計ソフトEZRを操作しながら理解できる。名義変数の解析から，連続変数の解析，傾向・相関の解析，多変量解析，生存期間の比較までを解説。これから統計を使いたい方に最適の一冊。　

目次はこちらから

医学界新聞プラス
［第4回］名義変数の解析をやってみよう②
『数式不要！はめ込み統計学　EZRでできる保健医療統計これだけ』より