新連載 Evidence-Based Medicineのための
実践統計学入門
山本和利 京都大学医学部附属病院総合診療部講師
Evidence―Based Medicine(EBM)は,直感や系統立たない臨床経験や病態生理のみを判断の根拠とせず,臨床研究からの事実をもとにして判断し,実践していく方法である。EBMを実践するために,臨床医は文献批判能力を身につけなければならない。その中には最低限の統計学の知識が含まれる。
世の中で起こったことは,真実,偶然,バイアスのいずれかに当てはまるEBMでは,「統計学的に問題がない(偶然ではない)から真実である」と判断する前に,バイアスがないかどうかに注意を払う。研究方法にバイアスがなく,偶然では説明できないとき初めてevidenceがあると言うことになる。
以前の連載「Study & Try医学生・研修医のための日常診療に役立つ臨床疫学」(本紙第2143~2199号)では,論文を読む時にバイアスがないか検討する方法を述べた。しかしながら,学会発表などを見ていると,まだまだバイアスを検討する以前に統計を間違って使っている例を見かける。そこで,今回は医師として必要と思われる統計学的知識について述べたい。
これまでに統計家の書いた本の大多数は数式が多く,医師には理解しにくい面がある。以下に示すのは,1996年6月にカナダのマクマスター大学で開かれた「医師のための統計学講座」に参加して得た教授法に,私なりの工夫を加えたものである。(山本和利)
(1) 代表値と散らばり
●事例ある集団21人の空腹時血糖値(FPG)は,それぞれ62,78,79,80,82,83,85,87,91,96,97,97,97,97,101,120,135,180,270,310,400mg/dlであった。この集団の血糖値を学会報告するとき,各個体から得られたデータを整理・要約し,平均値:129.14mg/dl,標準誤差(SE):±19.36mg/dlとした 1)。
●分布
記述統計学とは,分析対象とする集団の属性について完全に知ることのできる場合に,その分布をわかりやすく要約,整理するための手法である。全体でなく部分から推測する場合とは区別しなければならない。標本抽出の際にするような推測をあえてする必要はない。全体のデータは事実であり,推測の余地はないのである。
まず,医師は集団の臨床データの分布を正しく把握しなければならない。そのためには,臨床データのとりうる値をいくつかの階級に分け,それぞれの階級で度数を数えて,表にする(適切な階級数kはスタージェスの公式よりk=1+log2[総数]で求められる)。そして,データの分布の形をみるために度数分布表を柱状グラフ(ヒストグラム)にする。
このヒストグラムを言葉で説明するには,代表値と散らばりを記載することになる。代表値としては平均値(mean),中央値(median),最頻値(mode)といった表し方がある。散らばりの尺度としては範囲(range),四分位点(quartile),標準偏差(SD)などがある。これらのどれを用いるかは,ヒストグラムの型によって異なる。
●分散と標準偏差(SD)
各データと平均値との差を2乗して平均を求めたものを分散という。分散はS2という記号で表される。SDは分散の平方根をとったSで表される。
●ヒストグラムの型
ヒストグラムの山が1つの単峰型か2つの双峰型かで対応が異なる。双峰型であれば,通常,性質の異なるデータが混じりあっていることが多いので,患者の属性で層別した方がよい。
では単峰型の場合,事例のように平均値とSEを記述すればよいのであろうか。答は否である。平均値を用いてよいのはヒストグラムが左右対称(ベル型)の時である。左右が非対称(右に歪んだ分布,左に歪んだ分布)のときには,代表値としては中央値,最頻値を,散らばりの尺度としては範囲,四分位点で表すのがよい。また,ヒストグラムを描く前に,扱っている臨床データの測定尺度が名義尺度(例えば性別,病因など),順序尺度(癌の病期分類など),間隔尺度(体温,時刻など),比尺度(身長,体重など)のどれなのか把握しておくことはもちろんである。
これ以外に,データが正規分布に従うかをみるのに,市販されている正規確率紙を用いる方法がある。正規分布の場合には大きさの順に並べたプロットは直線になる。
●事例の検討
まず,空腹時血糖値データの測定尺度は比尺度である。データの分布の形をみるために,空腹時血糖値のとりうる値50~400mg/dlを7階級に分け,ヒストグラムを作成した(図1)。
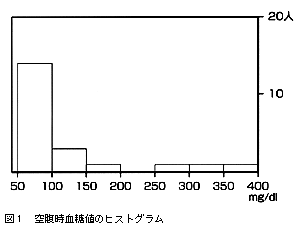
ヒストグラムの型は単峰型であるが,左右は非対称で右に歪んだ(山のすそ野が右側にのびた)分布をしている。ということはこの母集団における空腹時血糖値のヒストグラムはベル型ではないので,代表値として平均値を用いない方がよい(読む者が推測できないため)。代表値としては中央値:97mg/dl,散らばりの尺度としては範囲:62~400mg/dl,または第1四分位点(25パーセンタイル):82mg/dl,第3四分位点(75パーセンタイル):127.5mg/dlと表記した方がよい。これを図示したものを箱ひげ図(box plot)という(図2)。
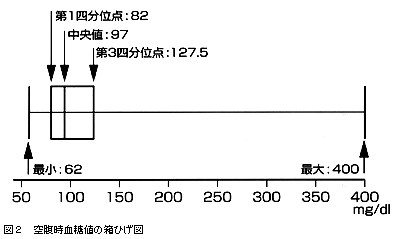
右に歪んだ分布としてはコレステロール値,中性脂肪値,アルカリフォスファターゼ値がある。ただし,事例の場合は右に歪んだが,一般に血糖値は正規分布をする。逆に左に歪んだ分布はヘモグロビン値で見られる2)。
ここでもう1つ注意点を述べよう。ヒストグラムが左右対称のベル型を示した場合は平均値を代表値とするが,集団の散らばりはSEではなく,SDを使用する(SEは平均値の推定に用いる)。事例に対して正規分布を仮定してSD(88.7mg/dl)から95%範囲(平均値±2SD)を求めようとすると,129.14-2×88.7=-48.3,129.14+2×88.7=306.5で,-48.3~306.5といったあり得ない数値をとることになる。
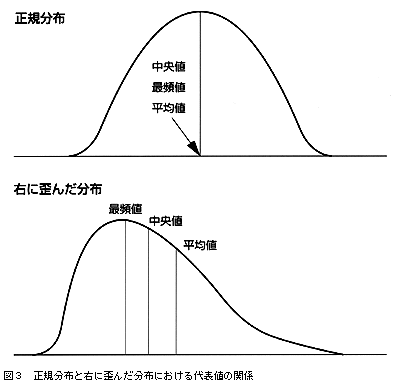
正規分布の場合,3つの代表値(平均値,中央値,最頻値)は一致する(図3)。SDがわかると1SDに68%の値が含まれ,2SDに95%含まれるのでベル型のひろがり方が推測できる。
●ここまでわかるとどの程度論文が読めるか?
New England Journal of Medicineの298~301巻に掲載された研究およびレビュー論文760本で用いられている統計手法を分類したところ,上で述べたような記述統計(パーセント,平均値,SD)に精通していれば,論文の58%は読めることがわかっている3)。
●まとめ
■データの分布の形をみるために度数分布表をヒストグラムにする。
■左右が非対称分布のときは,代表値としては中央値,最頻値を,散らばりの尺度としては範囲,四分位点で表すのがよい。
■左右対称のベル型分布のときには,代表値としては平均値を,散らばりの尺度としては標準偏差で表す。
謝辞
連載を始めるにあたり全編にわたって目を通して下さり,貴重な意見をいただいた富山医薬大統計・情報科学の折笠秀樹教授に深謝致します。
参考文献
- 1)
- Feinstein AR: Statistical Indexes for a Spectrum of Data, In Clinical Epidemiology The Architecture of Clinical Research. Philadelphia, Saunders: 90-117, 1985.
- 2)
- Fletcher RH, Fletcher S W, Wagner,EH: Abnormality, In Clinical Epidemiology The Essentials. 3rd ed. Baltimore, Williams & Wilkins: 19―42, 1996.
- 3)
- Emerson JD, Colditz GA: Use of statistical analysis in the New England Journal of Medicine, In Bailar III JC, Mosteller F ed. Medical Uses of Statistics. 2nd ed. Boston, NEJM Books: 45-57, 1992.
