連載 vidence-Based Medicineのための
実践統計学入門
山本和利 京都大学医学部附属病院総合診療部講師
(8) 重回帰分析(最終回)
●事例1
平均血圧値(mBP)と年齢,性別,ウエスト・ヒップ比(WHR),ボディ・マス・インデックス(BMI),血清インスリン値(IRI),空腹時血糖値(FPG),総コレステロール(TC),尿中Na排泄量(uNa/cre)との関係を調べるため30名を抽出し,表1のような結果を得た。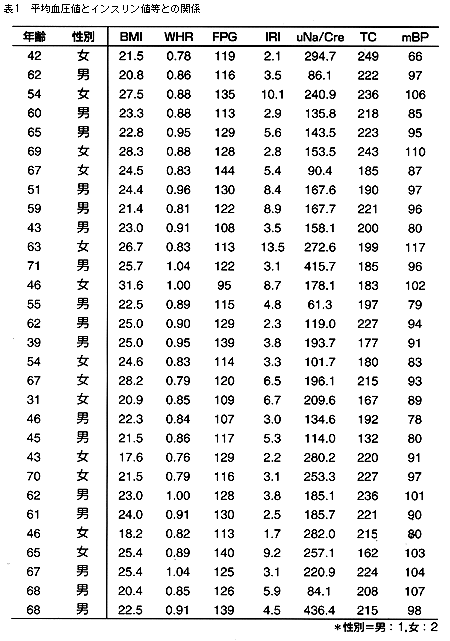
●重回帰分析
重回帰分析とは,従属変数(y)と独立変数(x)との関係を調べ,y=a+b1x1+b2x2+…biという関係式(重回帰式)を作成し,その式から独立変数の従属変数に及ぼす影響を検討する方法である。重回帰式の求め方は相関をみるときと同じ考え方を適用する。すなわち,(実測値Y-予測値y=a+b1x1+b2x2+……bi)2を最小となるようにb1,b2,biを求める方法である。事例のデータからmBPと年齢,IRIに注目してみよう。これらの間にはどのような関係があるだろうか。加齢とともにmBPは上昇するだろうか。IRIが高いとmBPは上昇するだろうか。mBPの上昇にはどちらが大きな要素であろうか。
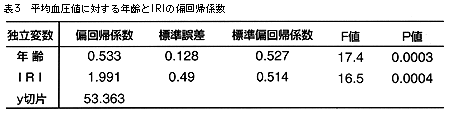
これらの疑問に答えるために,mBPをy,年齢をx1,IRIをx2として重回帰式を求めてみよう。手近のコンピュータ統計パッケージにデータを入力し,重回帰分析を指示すると,表2,3のような結果が表示される。

●重回帰の分散分析表
表3のy切片と偏回帰係数を代入すると,mBP=53.363+0.533×年齢+1.991×IRIという重回帰式が得られる。IRIが平均値をとったときには1歳年をとるごとにmBPは0.5mmHg上昇し,年齢が平均値をとったときにはIRIが1増えるとmBPは約2mmHg上昇することが推測される。では,「mBPの上昇には,偏回帰係数が大きいIRIのほうが年齢よりも影響が大きい」といってよいだろうか。実はそうではない。同じデータでも単位を変えることで偏回帰係数の値は大きく変わってしまう。そこで単位の影響を取り除くためにデータを標準化する方法が考え出された。
以前(連載第3回:2235号)にZ値を求めたやり方と同じように,独立変数も従属変数も平均を0,分散を1になるようにして,偏回帰係数を求める。そこで得られた値を標準偏回帰係数という。表2をみると年齢もIRIも標準偏回帰係数は約0.5でほぼ同等であることがわかる。すなわち,影響に差はないと推測できる。
この重回帰式がどのくらい「当てはまりがよい」かは寄与率(決定係数)をみるとよい。寄与率(R2)は(予測値の平方和)/(実測値の平方和)で,1に近いほど当てはまりがよいことを意味している。ただ,寄与率は独立変数の数が増えるにつれ,大きくなっていく。そこで,その欠点を改良するために自由度で調整した寄与率が表示される。その自由度調整済寄与率が一番大きな重回帰式が最も当てはまりがよいということになる。
●変数選択法
ここまでの重回帰分析の方法は,筆者が適当に独立変数として年齢とIRIを選んだに過ぎない。独立変数はどのように選んだらよいのだろうか。事例では8つの独立変数があるのですべて選べばよいのだろうか。ここで1つ注意しなければならないことがある。それは似たもの同士を一緒に入れてはいけないということである。すなわち,独立変数相互に高い相関がある場合には,どちらか一方を落とさないと信頼の低い重回帰式になってしまうからである(多重共線性)。落とす独立変数は従属変数との相関が低いほうとする。
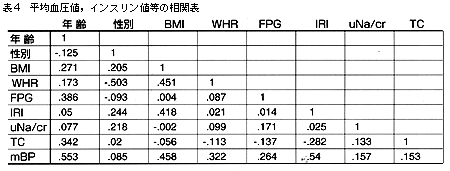
そこで,mBPを従属変数y,その他を独立変数xとし,個々の独立変数間の相関を検討してみる(表4)。
WHRとBMIとの間にはr=0.451,IRIとBMIとの間にはr=0.418の相関がある。r<0.5なので多重共線性を起こす可能性は少ないと考え,独立変数8個すべてを用いることにする。
独立変数を1個ずつ追加していく方法(前進選択法)と,すべて選択してF値の少ないものを減らしていくやり方(後進選択法)がある1)。最近のコンピュータ統計パッケージは両者を組み合わせたステップ・ワイズ法を採用しているものが多い。
次に,多変量解析のステップ・ワイズ法を選択する。そうするとコンピュータが8個の独立変数のうち,偏回帰係数のF値が4.0以上(自由度とαを何%にするかで変化する)で最大のF値を示す「年齢」を,有意な独立変数x1と判断し選び出す。残りの7個について同じことを繰り返す。
2回目には「IRI」が選択された。残りの6つはF値が4.0以下なので選択されなかった。取り込むための基準値を変えるとまったく違った選択になる。例えば,基準値を3.0以上とすると年齢,IRI,WHRが,2.0以上とすると年齢,IRI,WHR,総コレステロール(TC)が選択される。しかし,偏回帰係数が有意であるかどうかを自由度(回帰数,n-回帰数-1)のF表で検討すると,α=0.05で,TC,WHRとも棄却できないことがわかる。自由度調整寄与率は0.54(mBPの値は年齢とIRIで54%説明できる)で,最終的には表3と同じ結果が得られた。
●事例2
白人男性609名を9年間経過観察したデータを用いて,カテコラミン,年齢,心電図所見が,冠動脈疾患の発生をどの程度高めるか評価したい。コンピュータ統計パッケージのロジスティックモデルに当てはめたところ,α=-3.911,β1=0.652,β2=0.029,β3=0.342と表示された2)。●ロジスティック回帰分析
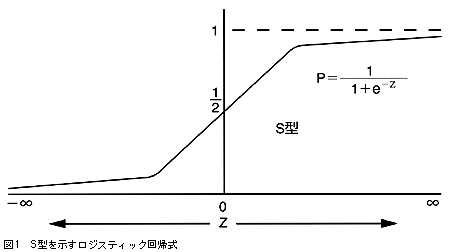
死亡または生存のように,0または1に置き換えられるデータを結果とするとき,ある前向き研究で一定時間後に死亡する確率をpとする。前向き研究では結果に影響する要因の相対危険度(RR)を知ることが主な目的となる。このRRを簡単に知ることができる方法がロジスティック回帰分析である。復習になるが,確率以外に不確実さを表す指標としてオッズがある。オッズはp/(1-p)つまり「ある結果が起こる確率(p)の,起こらない確率(1-p)に対する比率」と定義され,真陽性/偽陽性のことである。このオッズを自然対数化したものをZとする(正規分布のZ値とは別ものである)。そうするとZ=log[p/(1-p)]と表せる。これをpについて解くとp=1/{1+exp[-Z]}となる(exp[-Z]とはeの-Z乗のこと)。
なぜこのようなことをするかというと,こうするとPは0―1なのでロジット変換すると-∞-∞となり重回帰と同じようになるからである。この式を縦軸にP,横軸にZをとって描くと,Zの値が大きくなるにつれて右に上昇する図1のようなS字型になる。これらの性質と,自然対数の性質(簡単に「掛け算,割り算」を「足し算,割り算」に変換できる)を用いて,係数と表示された数字からRRを求めることができる。
予後因子でも,性別や検査結果の陽性,陰性のように0,1で表せる場合がある。Zを独立変数の関数で表し,Z=α+β1x1+β2x2+β3x3+…+βixiとする。
x1が1か0かの違いがある以外には他の予後因子x2,x3,…,xiがまったく同じという2つの場合を比較することを考えてみよう。例えば,事例で年齢と心電図所見がまったく同じでカテコラミン(CA)が高い(1)場合と,低い(0)場合を比較することを想定する。
具体的に計算するとZCA=1-ZCA=0=β1で,ZCA=1とZCA=0の差はβ1となる。はじめに定義したようにZはオッズを自然対数化したものなので,ZCA=1-ZCA=0は,カテコラミンが高い場合のオッズを低い場合のオッズで割ったもの(オッズ比)を自然対数化したものである(β1=log[オッズ比CA])。式を変換するとオッズ比CA=exp[β1]である。
このように,コンピュータが表示したβ1,β2,β3の数字から,カテコラミン,年齢,心電図所見のそれぞれの要因が冠動脈疾患の発生をどの程度高めるかを示すRRを,簡単に計算することができる(自然対数やeの計算ができる卓上計算機が必要である。コンピュータは表示しない)。ただし,ここで得られるのはあくまでオッズ比である(オッズ比は後ろ向き研究の指標である)。しかし,オッズ比はnが大きければRRに近似するので,前向き研究の結果を表示するときにはRRとして代用するわけである。
95%信頼区間を知りたければ,標準誤差(SE)を用いて簡単に計算できる。β1±1.96×SEを求め,eのβ1±1.96×SE乗すればよい。
年齢のように,連続変数の場合には,仮に40歳の患者を1とした場合の60歳の患者のRRを計算するということになる。事例では,40歳の患者を1とした場合の60歳の患者の冠動脈疾患のRRはexp[0.029×(60-40)]で1.79,カテコラミンが低い患者を1とした場合の,高い患者の冠動脈疾患のRRはexp[0.652]で1.92,心電図所見の正常患者を1とした場合の,異常患者の冠動脈疾患のRRはexp[0.342]で1.41であることがわかる。
●ここまでわかるとどの程度論文が読めるか?
重回帰分析に精通していればNew England Journal of Medicineの論文の92%は読めることがわかっている3)。●まとめ
■重回帰分析とは,y=a+b1x1+b2x2+…biという関係式を作成し,それから独立変数の従属変数に及ぼす影響を検討する方法である。■独立変数相互に高い相関がある場合には,従属変数との相関が低いほうを落とす必要がある。
■複数ある要因のオッズ比を知るにはロジスティック回帰分析を用いるのがよい。
参考文献
1)Dawson-Saunders B, Trapp RG: Statistical Methods for Multiple Variables, In Basic & Clinical Biostatistics, second edition, APPLETON & LANGE, Norwalk, 210-231, 1994.
2)Kleinbaum DG: Introduction to Logistic Regression, In Logistic Regression: A Self-Learning Text, Springer-Verlag, New York, 1-38,1994.
3)Emerson JD, Colditz GA: Use of statistical analysis in the New England Journal of Medicine, In Bailar III JC, Mosteller F, ed., Medical Uses of Statistics 2nd ed., NEJM Books, Boston, 45-57, 1992.
