連載 Evidence-Based Medicineのための

実践統計学入門

山本和利　京都大学医学部附属病院総合診療部講師

---

(5)　カイ２乗検定

●事例1

　ある病気に対する治療法Aの治癒率は6／8で75％，治療法Bの治癒率は2／6で33％であった^1）。治療法Aと治療法Bとの効果には有意な差があるだろうか？

●2×2分割表

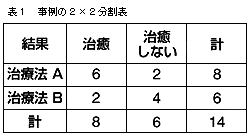
　母集団の分布がはっきりしない時に行なう検定をノンパラメトリック検定という。つまり，「正規分布をする母集団」などという仮定を抜きにして検定しようというのである。ノンパラメトリック検定にはさまざまな方法が知られている。ここでは最も単純な分割表を用いたカイ2乗検定について述べる。
　まず，2群の差が有意であるか検討するには，2×2分割表を書くのがよい（表1）。

●期待値の求め方

　治療法AとBに差がないと仮定すると，2×2表はどのようになるだろうか。
　表1から，治療した14人のうち8人が治癒しているので全体の治癒率は8／14である。治療法Aを受けている8人のうち，治癒する期待値は8×8／14＝4.57人と計算できる。
　Bの期待値も同様に計算できるが（6×8／14＝3.43人），2×2分割表は自由度1［（2－1）×（2－1）］なので，1つ計算すれば他の3つは合計から引き算で出せる。結果は表2のようになる。

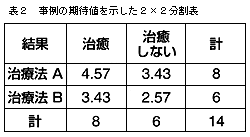
●カイ2乗検定

　期待値と現実の値との食い違いをその差で表し，その差の2乗を期待値で割り，すべてを加えたものをカイ2乗（χ²）値という。χ²＝Σ｛（現実の値－期待値）²／期待値｝となる。現実の値と期待値がすべて等しい場合にはχ²＝0となる。逆に現実の値と期待値との食い違いが大きければ大きいほど，χ²も大きくなる。この起こりにくさを確率的に表現して，帰無仮説の是非の判定に用いる。
　χ²分布はそもそも，標本の分散と母集団の分散の比に関する連続分布であり，連続変数としての標本の分散の検定に用いられた。が，今では質的データで，出現度数が十分に大きい場合には近似的にカイ2乗検定を利用している。

●カイ2乗を求める

　χ²＝Σ｛（現実の値－期待値）／期待値｝に事例の数値を代入してみよう。χ²＝（6－4.57）²／4.57＋（2－3.43）²／3.43＋（2－3.43）²／3.43＋（4－2.57）²／2.57＝2.43となる。
　自由度1のχ²分布表をみるとP値0.20でχ²が1.642，P値0.10でχ²が2.76である。χ²が2.43の時はP値が0.1～0.2の間にあることがわかる。よって，治療法AとBの治癒率には有意差は認められないと判断される。

●カイ2乗の公式

　表3のような一般の2×2分割表の場合には，χ²＝（ad－bc）²（a＋b＋c＋d）／（a＋b）（c＋d）（a＋c）（b＋d）＝（ad－bc）²×N／f₁f₂n₁n₂と表される。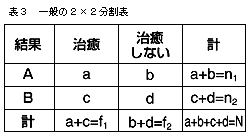

●イェーツの連続修正（χ²c）

　標本数が小さい場合には，イェーツの連続修正を用いるのがよいと統計の本には書かれている。これはχ²c＝［｜ad－bc｜－（N／2）］²N／f₁f₂n₁n₂と表す。これを用いるべきかどうかは統計家によって意見が分かれる。
　実際的にはN＜40か2×2表のa，b，c，dいずれかの期待値が5以下のときにはフィッシャー直接確率法（後出）を行ない，それ以外はカイ2乗検定を行なうのがよい。

●フィッシャーの正確検定

　治療法Aで治癒しない場合を考える。8人のうち1人だけ治癒しない可能性は8通り，残り7人のうちもう1人が治癒しない可能性は7通りで，つまり2人が治癒しない可能性は8×7通りである。順番を考慮する必要はないので2×1で割ると，8×7／2×1（₈C₂）＝28となる。
　治療法Bで治癒しない場合も同様に考える。6人のうち4人治癒しない可能性は6×5×4×3通りである。順番を考慮する必要はないので4×3×2×1で割ると6×5×4×3／4×3×2×1（₆C₄）＝15となる。
　治療法AとBとも効果は同じと仮定した場合に，治癒しない可能性は上と同様に考えて14人から6人を選ぶことになる。14×13×12×11×10×9／6×5×4×3×2×1（₁₄C₆）＝3003通りとなる。
　事例のような可能性Pを計算すると28×15／3003＝0.14となる。Pを一般式で書き換えるとp＝_n1C_b×_n2C_d／_NC_f2または（a＋b）！（c＋d）！（a＋c）！（b＋d）！／N!a!b！c！d！となる。
　事例において，とり得る場合のそれぞれのその効果の差（％）とP値を表4に示した。冒頭に提示した事例はP3に当たる。このときの治療法AとBの効果差は6／8－2／6＝0.75－0.33＝0.42（42％）である。治療法AとBが同じ効果であると仮定したときに，42％以上の差が現れる可能性はP₁＋P₂＋P₃＝0.159である。ここで終わると，BよりAがよいという片側検定しかしていないことになるので，逆の場合，すなわちAよりBが勝る－42％以上の差が現れる可能性P₄＋P₅＝0.121を加える必要がある。最終的にはP＝0.159＋0.121＝0.280となり，治療法Aと治療法Bとの効果には有意な差はないことがわかる。

　有意差が現れるのはどのくらいの差であろうか。事例に戻って「治療法Aの治癒率は7／8で87.5％，治療法Bの治癒率は1／6で16.7％であった」場合にはどうであろうか。表4より，71％以上の差がある可能性はP₁＋P₂＋P₅で，0.0003＋0.016＋0.009＝0.0253と計算でき，ここではじめて統計的に有意な差となる。
　手近の統計ソフトに事例を入力してみる。フィッシャーの正確検定を選択すると2×2表が現れる。a，b，c，dそれぞれに値を入力すると，P＝0.277と結果だけが表示される。
　参考までに，カイ2乗検定（事例では標本数が少ないのでフィッシャーの正確検定がよいのは承知の上で）を選択すると，分割表を何×何にするか聞いてくる。2×2表を選んで，上と同様に入力すると，自由度1でカイ2乗値＝1.027，P＝0.311と表示される。

●事例2

　放射線科医AとBに，n枚のレントゲン写真を正常か異常かに判定してもらった。「A，Bとも正常」と判定したものはa枚，「Aは正常でBが異常」はb枚，「Aが異常でBが正常」はc枚，「A，Bとも異常」と判定したものはd枚であった＄上始＄1)＄上終＄。AとBの読影に有意差があるかどうかをどのように検討したらよいか？

●McNemarカイ2乗検定

　1標本を前後で評価する場合や，1標本を2名で評価してその違いを見る場合には，カイ2乗検定ではなく，McNemarカイ2乗検定を用いる。事例を分割表にすると表5のようになる。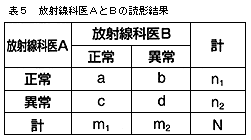

　両者の意見が一致しているaとdは，違いをみるために考慮する必要がない。そこでbとcの違いを検討することになる。放射線科医AとBの能力が同じと仮定すると，b，cの期待値はともに（b＋c）／2である。
　McNemarカイ2乗＝Σ｛（現実の値－期待値）²／期待値｝＝｛（b＋c）／2－（b）｝²／（b＋c）／2＋｛（b＋c）／2－（c）｝²／（b＋c）／2＝（b－c）²／（b＋c）となる。数が少ない場合にはイェーツの連続修正を用いる。McNemaχ²c＝（｜b－c｜－1）²／（b＋c）と表される。手近の統計ソフトではイェーツの連続修正をした式をもとに結果が打ち出された。
　事例をカイ2乗検定しようとすると表6のように分割表を書き直すことになる。ふつうの分割表との違いは1つのデータが2回登録されている点である（その点からすると正しい分画表とは言えない）。

●ここまでわかるとどの程度，論文が読めるか？

　分割表に精通していればNew England Journal of Medicine論文の66％，ノンパラメトリック検定に精通していれば70％は読めることがわかっている^2）。

●まとめ

■分布が不明なデータの2群差を検討するには2×2分割表を書くのがよい。

■標本数が小さい場合（N＜40か2×2表のa，b，c，dいずれかの期待値が5以下）にはフィッシャーの正確検定を行ない，それ以外はカイ2乗検定を用いるのがよい。

参考文献
1）Feinstein AR: Stochastic Contrasts, In Clinical Epidemiology The Architecture of Clinical Research, Philadelphia, Saunders, 130-169,1985.
2）Emerson JD, Colditz GA: Use of statistical analysis in the New England Journal of Medicine, In Bailar III JC, Mosteller F, ed., Medical Uses of Statistics 2nd ed.,Boston, NEJM Books, 45-57,1992.