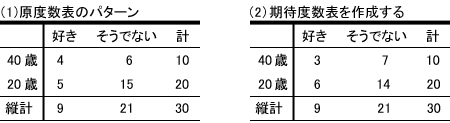
（4）　（3）で得られた符号にしたがって，原度数に対して期待度数から離れる方向で度数表（2×2分割表）を求める。
具体的には，周辺度数を固定したまま，原度数表と期待度数表の各度数の差がさらに大きくなるように各内部度数から1ずつ増減した2×2分割表を作成する。

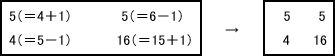
さらに，4つの内部度数のうち，いずれか1つの度数が0となるまで同じ操作を繰り返して，2×2分割表を作成する。

その結果，本例題では，6組（原度数表を含む）の2×2分割表が得られる。

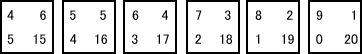
これらの6組のそれぞれの確率を，95頁の公式（3．12'）に従って計算し，合計する。

それぞれの確率は 0.2275673， 0.0853378， 0.0167329， 0.0015936， 0.0000629， 0.0000007 となりこれらを合計した結果，片側確率は0.3312952が得られる。

　この値は，有意差の有無を判定する5％よりも大きい。よって有意差なしと判定する。
（この場合のP値は片側検定の方法＜43頁＞で判定する。

　以上の計算からわかるように，直接確率計算法は，確かに正確な計算方法ではあるが，計算が厄介 なので，一般にはイェーツの修正による方法で計算を行う。