臨床研究を行う際，あるいは論文等を読む際，統計学の知識を持つことは必須です。
　本連載では，統計学が敬遠される一因となっている数式をなるべく使わない形で，論文などに多用される統計，医学研究者が陥りがちなポイントとそれに対する考え方について紹介し，臨床研究分野のリテラシーの向上をめざします。

　研究計画の策定時に，データをどれくらいの数の被験者から集めてくればよいのか頭を悩ませたり，実験マウスを1群10匹にするのか，5匹にするのかで迷ったりしたことはないでしょうか？　

　以前本紙に寄稿した際（第2912号）に触れたように，サンプル数が多ければ多いほど解析の精度が上がり，それに伴いP値は小さくなります。極端に言えば，臨床的に意味のないどんなに小さな差でも，サンプル数を増やせばいつかは統計的には有意となります。解析の精度が高いほど科学的にはよいと言えるでしょう。

　しかし実際には，多くの被験者を安全性の確認されていない新薬の危険に不必要にさらすべきでないという倫理的な観点と，研究にかかるコストを必要以上に大きくしないという経済的な観点から，基礎研究，臨床研究を問わず米国立衛生研究所（NIH）のグラント申請時には，常に"必要最低限"のサンプル数を見積もることが要求されます。今回は，研究の際にサンプル数をどのように決定するのかを，お話ししたいと思います。

サンプル数はどのように決定するのか？

　P値とは，新薬にまったく効果がないにもかかわらず，あたかも効果があるような結果になってしまうエラーの確率のことです。このエラーが5％未満程度であれば許そうという慣習的なルールによって，P値が5％より小さければ新薬に効果があると判断されます。ただしサンプル数を研究開始前に決めずに何度も仮説検定を繰り返し，P値が5％より小さくなるまでデータを取り続けると，実はこのエラーが起きる確率は5％より高くなり，ルール違反となります（多重検定の問題点については次回詳しく説明する予定です）。

　サンプル数は通常，研究プロトコルに表記され，その定められた数に到達し研究を終了して初めて主要評価項目の解析が行われます。もちろん最近のランダム化比較試験では，研究途中で中間解析などを繰り返し行うことも多いのですが，その場合はこのエラーが大きくならないよう，それぞれの中間解析の有意水準を厳しくとるなど細かな配慮が必要とされます（中間解析についても別の回で紹介する予定です）。

　ランダム化比較試験結果のまとめ方を示した国際的なガイドラインであるCONSORT声明では，研究結果をまとめた論文にも研究計画時にどのようにサンプル数を決定したのかを記載するよう定めています（註1）。ですから，一度決められたサンプル数を容易に変更することはできません。

　研究計画を策定する際には，例えば新薬と既存薬間で血圧の平均値の差が5 mmHgであるというように，研究によって起こり得る結果を研究開始前に推測してサンプル数を計算します。推測された差が大きければ，比較的小さなサンプル数でも有意差が出ますが，差が小さければ大きなサンプル数が必要となります。

　この推測を誤り，実際よりも差が大きく出ると見積もってしまうと，サンプル数不足となって解析の精度が落ちてしまい，せっかく臨床的に意味のある差でも統計的に有意差が確認できないといったジレンマに陥ってしまうかもしれません。ですから，予測を行う際には過去の文献や試験的なパイロット研究のデータなどを基に，慎重に行わなければなりません。

　この見積もりさえうまくできれば，あとは既存のソフトで簡単にサンプル数を計算することができます。最近ではnQuery AdvisorやPASSなど多くのソフトウェアが出回っています。しかし，それらのソフトウェアの多くは数万円以上のコストがかかります。

　ここでは，私の所属するヴァンダービルト大学医療統計学部で提供している無料のソフトを紹介します。「Power and Sample Size Calculation」（PS）と名付けられたこのソフトは，ホームページ（註2）からすぐにダウンロードできます。

サンプル数の計算方法

　さあ，準備はよいですか？　早速「新規の鎮静薬を投与した50 人の患者」と「投与しない50 人の患者」間で血圧を比較する研究のサンプル数を計算してみましょう。

　図は，PSのメイン画面を示したものです。画面上段（図中（1））にSurvival（生存率解析），t-test（スチューデントのt検定と対応のあるt検定），Regression（線形回帰），Dichotomous（アウトカムが2値変数）など，検定法が並んでいます。サンプル数計算は検定法によって異なる数式から求められます。どの検定法を使用するか迷っている方は，本連載第1回（第2927号），2回（第2933号）で紹介した単変量，多変量の統計テストの選択方法をご参照ください。

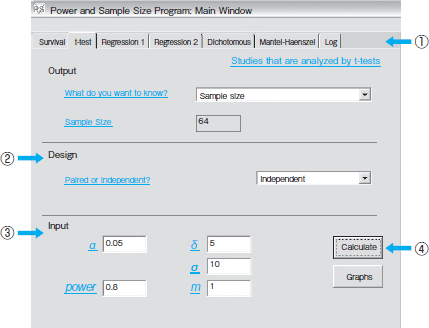図　「Power and Sample Size Calculation」（PS）のメイン画面

　この例では，アウトカム血圧は連続変数，比較する群の数が2 群であることから，t-testを選択しました。"Design"の項目（図中（2））でIndependentを選択すると，対応のない2群間の比較となり，検定法はスチューデントのt検定が用いられます。比較群に対応がある場合にはPairedを選択すると，対応のあるt検定が選択されます。

　次に"Input"の項目（図中（3））ですが，αとは先に述べた，差がないのに誤って"差がある"と言ってしまうエラーのことで，一般に「1型エラー」と呼ばれています。これは「有意水準」とも呼ばれ，通常5％を使用します。この有意水準には両側と片側がありますが，ほとんどの場合両側を使用しなければなりません。ちなみに本当に差があるときに誤って"差がない"と言ってしまうエラーは「2型エラー」と呼ばれます。

　続いてPowerとは2型エラーの逆で，本当に差があるときに正しく"差がある"と判断する確率です。先述した解析の精度を表し，「検出力」（パワー）と呼ばれます。パワーは大きいほどよく，慣習的に80－90％が使われています。パワーが上がればP値は小さくなります。

　さらにδとは，検出したい2 群間の差。σとはアウトカム（この例では血圧）の標準偏差（SD）で，それぞれの群で別々に計算して求めます。mは2群のサンプル数の比であり，2群間のサンプル数が同じ場合は1と定義されます。例えば，コントロール群を介入群の2 倍の大きさでとるデザインでは，「m＝2」となります。

　これらの値をそれぞれ入力してCalculateのボタン（図中（4））を押すと，研究に最低限必要なサンプル数が算出されます。前述したように，通常αは5％，Powerは80％または90％を使い，mはデザインによって自分で決定できるので，事前に調査が必要なパラメータは「検出したい最低限の2 群間」の差（δ）と「標準偏差」（σ）の2 つのみで，文献やパイロットデータなどから割り出します。

　先ほど例に挙げた研究では，「糖尿病患者の血圧のSDが10 mmHgで，新薬では既存薬に比べ血圧を平均で5 mmHg減らすことが臨床的に最低限必要な意味のある差だと考えられる」と仮定した場合，検出力を80％以上とするためには，それぞれの群に最低64人の患者が必要となります。

　回帰分析を使った多変量解析のサンプル数は，前回紹介したように，回帰モデルに入れる暴露因子の数によって決まるので，そちらをご参照ください。このように，サンプル数の計算は自分で簡単に行えるので，ぜひ試してみてください。

（つづく）

註1）CONSORTホームページ
註2）ヴァンダービルト大学「Power and Sample Size Calculation」ホームページ